
The notion that a dollar today is preferable to a dollar some time in the future is intuitive enough for most people to grasp without the use of models and mathematics. The principles of present value provide more backing for this statement, however, and enable us to calculate exactly how much a dollar some time in the future is worth in today’s dollars and to move cash flow across time. Present value is a concept that is intuitively appealing, simple to compute, and has a wide range of applications. It is useful in decision making ranging from simple personal decisions - buying a house, saving for a child's education and estimating income in retirement, to more complex corporate financial decisions - picking projects in which to invest as well as the right financing mix for these projects.
Time Lines and Notation
Dealing with cash flows that are at different points in time is made easier using a time line that shows both the timing and the amount of each cash flow in a stream. Thus, a cash flow stream of $100 at the end of each of the next 4 years can be depicted on a time line like the one depicted in Figure 3.1.

In the figure, 0 refers to right now. A cash flow that occurs at time 0 is therefore already in present value terms and does not need to be adjusted for time value. A distinction must be made here between a period of time and a point in time. The portion of the time line between 0 and 1 refers to period 1, which, in this example, is the first year. The cash flow that occurs at the point in time "1" refers to the cash flow that occurs at the end of period 1. Finally, the discount rate, which is 10% in this example, is specified for each period on the time line and may be different for each period. Had the cash flows been at the beginning of each year instead of at the end of each year, the time line would have been redrawn as it appears in Figure 3.2.

Note that in present value terms, a cash flow that occurs at the beginning of year 2 is the equivalent of a cash flow that occurs at the end of year 1.
Cash flows can be either positive or negative; positive cash flows are called cash inflows and negative cash flows are called cash outflows. For notational purposes, we will assume the following for the chapter that follows:
Notation
Stands for
PV
Present Value
FV
Future Value
A
Annuity: Constant cash flows over several periods
r
Discount Rate
g
Expected growth rate
n
The Intuitive Basis for Present Value
There are three reasons why a cash flow in the future is worth less than a similar cash flow today.
(1) Individuals prefer present consumption to future consumption. People would have to be offered more in the future to give up present consumption. If the preference for current consumption is strong, individuals will have to be offered much more in terms of future consumption to give up current consumption, a trade-off that is captured by a high "real" rate of return or discount rate. Conversely, when the preference for current consumption is weaker, individuals will settle for much less in terms of future consumption and, by extension, a low real rate of return or discount rate.
(2) When there is monetary inflation, the value of currency decreases over time. The greater the inflation, the greater the difference in value between a cash flow today and the same cash flow in the future.
(3) A promised cash flow might not be delivered for a number of reasons: the promisor might default on the payment, the promisee might not be around to receive payment; or some other contingency might intervene to prevent the promised payment or to reduce it.. Any uncertainty (risk) associated with the cash flow in the future reduces the value of the cashflow.
The process by which future cash flows are adjusted to reflect these factors is called discounting, and the magnitude of these factors is reflected in the discount rate. The discount rate incorporates all of the above mentioned factors. In fact, the discount rate can be viewed as a composite of the expected real return (reflecting consumption preferences in the aggregate over the investing population), the expected inflation rate (to capture the deterioration in the purchasing power of the cash flow) and the uncertainty associated with the cash flow.
The Mechanics of Time Value
The process of discounting future cash flows converts them into cash flows in present value terms. Conversely, the process of compounding converts present cash flows into future cash flows.
Time Value Principle 1: Cash flows at different points in time cannot be compared and aggregated. All cash flows have to be brought to the same point in time before comparisons and aggregations can be made.
There are five types of cash flows - simple cash flows, annuities, growing annuities, perpetuities and growing perpetuities, which we discuss below.
Simple Cash Flows
A simple cash flow is a single cash flow in a specified future time period; it can be depicted on a time line:

where CFt = the cash flow at time t.
This cash flow can be discounted back to the present using a discount rate that reflects the uncertainty of the cash flow. Concurrently, cash flows in the present can be compounded to arrive at an expected future cash flow.
I. Discounting a Simple Cash Flow
Discounting a cash flow converts it into present value dollars and enables the user to do several things. First, once cash flows are converted into present value dollars, they can be aggregated and compared. Second, if present values are estimated correctly, the user should be indifferent between the future cash flow and the present value of that cash flow. The present value of a cash flow can be written as follows
Present Value of Simple Cash Flow =![]()
where
CFt = Cash Flow at the end of time period t
r = Discount Rate
Other things remaining equal, the present value of a cash flow will decrease as the discount rate increases and continue to decrease the further into the future the cash flow occurs.
Illustration : Discounting a Cash Flow
Assume that you own Infosoft, a small software firm. You are currently leasing your office space, and expect to make a lump sum payment to the owner of the real estate of $500,000 ten years from now. Assume that an appropriate discount rate for this cash flow is 10%. The present value of this cash flow can then be estimated —
Present Value of Payment = ![]() = $192,772
= $192,772
This present value is a decreasing function of the discount rate, as illustrated in Figure 3.4.

II. Compounding a Cash Flow
Current cash flows can be moved to the future by compounding the cash flow at the appropriate discount rate.
Future Value of Simple Cash Flow = CF0 (1+ r)t
where
CF0 = Cash Flow now
r = Discount rate
Again, the compounding effect increases with both the discount rate and the compounding period.
Illustration: The Power of Compounding - Stocks, Bonds and Bills
As the length of the holding period is extended, small differences in discount rates can lead to large differences in future value. In a study of returns on stocks and bonds between 1926 and 1997, Ibbotson and Sinquefield found that stocks on the average made 12.4%, treasury bonds made 5.2%, and treasury bills made 3.6%. Assuming that these returns continue into the future, Table 3.1 provides the future values of $ 100 invested in each category at the end of a number of holding periods - 1 year, 5 years, 10 years, 20 years, 30 years, and 40 years.
Table 3.1: Future Values of Investments - Asset Classes
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The differences in future value from investing at these different rates of return are small for short compounding periods (such as 1 year) but become larger as the compounding period is extended. For instance, with a 40-year time horizon, the future value of investing in stocks, at an average return of 12.4%, is more than 12 times larger than the future value of investing in treasury bonds at an average return of 5.2% and more than 25 times the future value of investing in treasury bills at an average return of 3.6%.
The Rule of 72 : A Short Cut to estimating the Compounding Effect
In a pinch, the rule of 72 provides an approximate answer the question "How quickly will this amount double in value?" by dividing 72 by the discount or interest rate used in the analysis. Thus, a cash flow growing at 6% a year will double in value in approximately 12 years, while a cash flow growing at 9% will double in value in approximately 8 years.
III. The Frequency of Discounting and Compounding
The frequency of compounding affects both the future and present values of cash flows. In the examples above, the cash flows were assumed to be discounted and compounded annually, i.e., interest payments and income were computed at the end of each year, based on the balance at the beginning of the year. In some cases, however, the interest may be computed more frequently, such as on a monthly or semi-annual basis. In these cases, the present and future values may be very different from those computed on an annual basis; the stated interest rate, on an annual basis, can deviate significantly from the effective or true interest rate. The effective interest rate can be computed as follows
Effective Interest Rate = ![]()
where
n = number of compounding periods during the year (2=semiannual; 12=monthly)
For instance, a 10% annual interest rate, if there is semiannual compounding, works out to an effective interest rate of
Effective Interest Rate = 1.052 - 1 = .10125 or 10.25%
As compounding becomes continuous, the effective interest rate can be computed as follows
Effective Interest Rate = expr - 1
where
exp = exponential function
r = stated annual interest rate
Table 3.2 provides the effective rates as a function of the compounding frequency.
Table 3.2: Effect of Compounding Frequency on
Effective Interest Rates
Frequency
Rate
t
Formula
Effective Annual Rate
Annual
10%
1
1.10-1
10%
Semi-annual
10%
2
(1+.10/2)2-1
10.25%
Monthly
10%
12
(1+.10/12)12-1
10.47%
Daily
10%
365
(1+.10/365)365-1
10.5156%
Continuous
10%
exp(.10)-1
10.5171%
As you can see, compounding becomes more frequent, the effective rate increases, and the present value of future cash flows decreases.
Annuities
An annuity is a constant cash flow that occurs at regular intervals for a fixed period of time. Defining A to be the annuity, the time line for an annuity may be drawn as follows:
An annuity can occur at the end of each period, as in this time line, or at the beginning of each period.
I. Present Value of an End-of-the-Period Annuity
The present value of an annuity can be calculated by taking each cash flow and discounting it back to the present and then adding up the present values. Alternatively, a formula can be used in the calculation. In the case of annuities that occur at the end of each period, this formula can be written as

where
A = Annuity
r = Discount Rate
n = Number of years
Accordingly, the notation we will use in the rest of this book for the present value of an annuity will be PV(A,r,n).
Illustration : Estimating the Present Value of Annuities
Assume again that you are the owner of Infosoft, and that you have a choice of buying a copier for $10,000 cash down or paying $ 3,000 a year for 5 years for the same copier. If the opportunity cost is 12%, which would you rather do?

The present value of the installment payments exceeds the cash-down price; therefore, you would want to pay the $10,000 in cash now.
Alternatively, the present value could have been estimated by discounting each of the cash flows back to the present and aggregating the present values as illustrated in Figure 3.5.

Illustration : Present Value of Multiple Annuities
Suppose you are the pension fund consultant to The Home Depot, and that you are trying to estimate the present value of its expected pension obligations, which amount in nominal terms to the following:
Years Annual Cash Flow
1 - 5 $ 200.0 million
6 - 10 $ 300.0 million
11 - 20 $ 400.0 million
If the discount rate is 10%, the present value of these three annuities can be estimated as follows:
Present Value of first annuity = $ 200 million * PV (A, 10%, 5) = $ 758 million
Present Value of second annuity = $ 300 million * PV (A,10%,5) / 1.105 = $ 706 million
Present Value of third annuity = $ 400 million * PV (A,10%,10) / 1.1010 = $ 948 million
The present values of the second and third annuities can be estimated in two steps. First, the standard present value of the annuity is computed over the period that the annuity is received. Second, that present value is brought back to the present. Thus, for the second annuity, the present value of $ 300 million each year for 5 years is computed to be $1,137 million; this present value is really as of the end of the fifth year. It is discounted back 5 more years to arrive at today’s present value which is $ 706 million.
Cumulated Present Value = $ 758 million+$706 million+$948 million = $2,412 million
II. Amortization Factors - Annuities Given Present Values
In some cases, the present value of the cash flows is known and the annuity needs to be estimated. This is often the case with home and automobile loans, for example, where the borrower receives the loan today and pays it back in equal monthly installments over an extended period of time. This process of finding an annuity when the present value is known is examined below —

Illustration : Calculating The Monthly Payment On A House Loan
Suppose you are trying to borrow $200,000 to buy a house on a conventional 30-year mortgage with monthly payments. The annual percentage rate on the loan is 8%. The monthly payments on this loan can be estimated using the annuity due formula:
Monthly interest rate on loan = APR/ 12 = 0.08/12 = 0.0067

This monthly payment is an increasing function of interest rates. When interest rates drop, homeowners usually have a choice of refinancing, though there is an up-front cost to doing so. We examine the question of whether or not to refinance later in this chapter.
III. Future Value Of End-Of-The-Period Annuities
In some cases, an individual may plan to set aside a fixed annuity each period for a number of periods and will want to know how much he or she will have at the end of the period. The future value of an end-of-the-period annuity can be calculated as follows:
![]()
Thus, the notation we will use throughout this book for the future value of an annuity will be FV(A,r,n).
Illustration : Individual Retirement Accounts (IRA)
Individual retirement accounts (IRAs) allow some tax payers to set aside $2,000 a year for retirement and exempts the income earned on these accounts from taxation. If an individual starts setting aside money in an IRA early in her working life, the value at retirement can be substantially higher than the nominal amount actually put in. For instance, assume that this individual sets aside $2,000 at the end of every year, starting when she is 25 years old, for an expected retirement at the age of 65, and that she expects to make 8% a year on her investments. The expected value of the account on her retirement date can be estimated as follows:
![]()
The tax exemption adds substantially to the value because it allows the investor to keep the pre-tax return of 8% made on the IRA investment. If the income had been taxed at say 40%, the after-tax return would have dropped to 4.8%, resulting in a much lower expected value:
![]()
As you can see, the available funds at retirement drops by more than 55% as a consequence of the loss of the tax exemption.
IV. Annuity Given Future Value
Individuals or businesses who have a fixed obligation to meet or a target to meet (in terms of savings) some time in the future need to know how much they should set aside each period to reach this target. If you are given the future value and are looking for an annuity - A(FV,r,n) in terms of notation:
![]()
Illustration : Sinking Fund Provision on a Bond
In any balloon payment loan, only interest payments are made during the life of the loan, while the principal is paid at the end of the period. Companies that borrow money using balloon payment loans or conventional bonds (which share the same features) often set aside money in sinking funds during the life of the loan to ensure that they have enough at maturity to pay the principal on the loan or the face value of the bonds. Thus, a company with bonds with a face value of $100 million coming due in 10 years would need to set aside the following amount each year (assuming an interest rate of 8%):
![]()
The company would need to set aside $6.9 million at the end of each year to ensure that there are enough funds ($10 million) to retire the bonds at maturity.
V. Effect Of Annuities At The Beginning Of Each Year
The annuities considered thus far in this chapter are end-of-the-period cash flows. Both the present and future values will be affected if the cash flows occur at the beginning of each period instead of the end. To illustrate this effect, consider an annuity of $ 100 at the end of each year for the next 4 years, with a discount rate of 10%.

Contrast this with an annuity of $100 at the beginning of each year for the next four years, with the same discount rate.

Since the first of these annuities occurs right now, and the remaining cash flows take the form of an end-of-the-period annuity over 3 years, the present value of this annuity can be written as follows:

In general, the present value of a beginning-of-the-period annuity over n years can be written as follows:

This present value will be higher than the present value of an equivalent annuity at the end of each period.
The future value of a beginning-of-the-period annuity typically can be estimated by allowing for one additional period of compounding for each cash flow:
![]()
This future value will be higher than the future value of an equivalent annuity at the end of each period.
Illustration : IRA - Saving At The Beginning Of Each Period Instead Of The End
Consider again the example of an individual who sets aside $2,000 at the end of each year for the next 40 years in an IRA account at 8%. The future value of these deposits amounted to $ 518,113 at the end of year 40. If the deposits had been made at the beginning of each year instead of the end, the future value would have been higher:
![]()
As you can see, the gains from making payments at the beginning of each period can be substantial.
Growing Annuities
A growing annuity is a cash flow that grows at a constant rate for a specified period of time. If A is the current cash flow, and g is the expected growth rate, the time line for a growing annuity appears as follows —

Note that, to qualify as a growing annuity, the growth rate in each period has to be the same as the growth rate in the prior period.
The Process Of Discounting
In most cases, the present value of a growing annuity can be estimated by using the following formula —

The present value of a growing annuity can be estimated in all cases, but one - where the growth rate is equal to the discount rate. In that case, the present value is equal to the nominal sums of the annuities over the period, without the growth effect.
PV of a Growing Annuity for n years (when r=g) = n A
Note also that this formulation works even when the growth rate is greater than the discount rate.
![]() This spreadsheet allows you to estimate the present value of a growing annuity
This spreadsheet allows you to estimate the present value of a growing annuity
Illustration: The Value Of A Gold Mine
Suppose you have the rights to a gold mine for the next 20 years, over which period you plan to extract 5,000 ounces of gold every year. The current price per ounce is $300, but it is expected to increase 3% a year. The appropriate discount rate is 10%. The present value of the gold that will be extracted from this mine can be estimated as follows:

The present value of the gold expected to be extracted from this mine is $16.146 million; it is an increasing function of the expected growth rate in gold prices. Figure 3.6 illustrates the present value as a function of the expected growth rate.
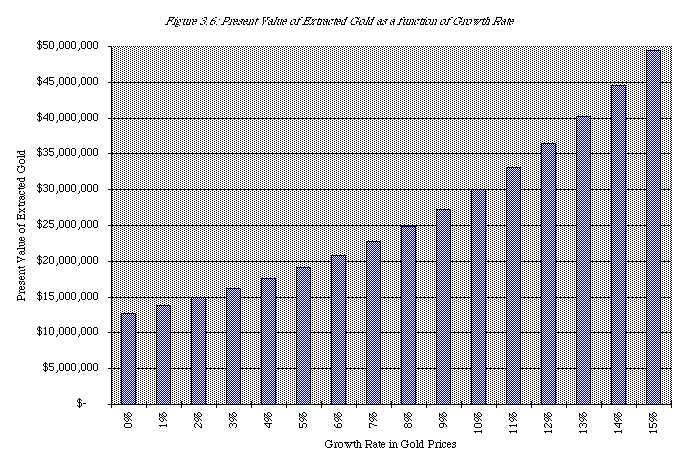
+Concept Check: If both the growth rate and the discount rate increase by 1%, will the present value of the gold to be extracted from this mine increase or decrease? Why?
Perpetuities
A perpetuity is a constant cash flow at regular intervals forever. The present value of a perpetuity can be written as
![]()
where A is the perpetuity. The future value of a perpetuity is infinite.
Illustration: Valuing a Console Bond
A console bond is a bond that has no maturity and pays a fixed coupon. Assume that you have a 6% coupon console bond. The value of this bond, if the interest rate is 9%, is as follows:
Value of Console Bond = $60 / .09 = $667
The value of a console bond will be equal to its face value (which is usually $1000) only if the coupon rate is equal to the interest rate.
Growing Perpetuities
A growing perpetuity is a cash flow that is expected to grow at a constant rate forever. The present value of a growing perpetuity can be written as:
![]()
where CF1 is the expected cash flow next year, g is the constant growth rate and r is the discount rate.
While a growing perpetuity and a growing annuity share several features, the fact that a growing perpetuity lasts forever puts constraints on the growth rate. It has to be less than the discount rate for this formula to work.
Illustration: Valuing a Stock with Stable Growth in Dividends
In 1992, Southwestern Bell paid dividends per share of $2.73. Its earnings and dividends had grown at 6% a year between 1988 and 1992 and were expected to grow at the same rate in the long term. The rate of return required by investors on stocks of equivalent risk was 12.23%.
Current Dividends per share = $2.73
Expected Growth Rate in Earnings and Dividends = 6%
Discount Rate = 12.23%
Value of Stock = $2.73 *1.06 / (.1223 -.06) = $46.45
As an interesting aside, the stock was actually trading at $70 per share. This price could be justified by using a higher growth rate. The value of the stock is graphed in figure 3.7 as a function of the expected growth rate.

The growth rate would have to be approximately 8% to justify a price of $70. This growth rate is often referred to as an implied growth rate.
Combinations and Uneven Cash Flows
In the real world, a number of different types of cash flows may exist simultaneously, including annuities, simple cash flows, and sometimes perpetuities: Some examples are discussed below.

Since coupons are fixed and paid at regular intervals, they represent an annuity, while the face value of the bond is a single cash flow that has to be discounted separately. The value of a straight bond can then be written as follows:
Value of Straight Bond = Coupon (PV of an Annuity for the life of the bond)
+ Face Value (PV of a Single Cash Flow)
Illustration: The Value of a Straight Bond
Say you are trying to value a straight bond with a 15-year maturity and a 10.75% coupon rate. The current interest rate on bonds of this risk level is 8.5%.
PV of cash flows on bond = 107.50* PV(A,8.5%,15 years) + 1000/1.08515 = $ 1186.85
If interest rates rise to 10%,
PV of cash flows on bond = 107.50* PV(A,10%,15 years)+ 1000/1.1015 = $1,057.05
Percentage change in price = ($1057.05—$1186.85)/$1186.85 = — 10.94%
If interest rate fall to 7%,
PV of cash flows on bond = 107.50* PV(A,7%,15 years)+ 1000/1.0715 = $1,341.55
Percentage change in price = ($1341.55—$1186.85)/$1186.85 = +13.03%
This asymmetric response to interest rate changes is called convexity.
Illustration: Contrasting Short Term Versus Long Term Bonds
Now say you are valuing four different bonds - 1 year, 5 year, 15 year, and 30 year- with the same coupon rate of 10.75%. Figure 3.8 contrasts the price changes on these three bonds as a function of interest rate changes.

Bond Pricing Proposition 1: The longer the maturity of a bond, the more sensitive it is to changes in interest rates.
Illustration: Contrasting Low Coupon And High Coupon Bonds
Suppose you are valuing four different bonds, all with the same maturity - 15 years — but different coupon rates - 0%, 5%, 10.75% and 12%. Figure 3.9 contrasts the effects of changing interest rates on each of these bonds.

Bond Pricing Proposition 2: The lower the coupon rate on the bond, the more sensitive it is to changes in interest rates.

The dividends over the high growth period represent a growing annuity, while the dividends after that satisfy the conditions of a growing perpetuity. The value of the stock can thus be written as the sum of the two present values.

Growing Annuity Growing Perpetuity - discounted back
where
P0 = Present Value of expected dividends
g = Extraordinary growth rate for the first n years (n = High growth period)
gn = Growth rate forever after year n
D0 = Current dividends per share
Dt = Dividends per share in year t
r = Required rate of return -> Discount Rate
Illustration : The Value of a High Growth Stock
In 1992. Eli Lilly had earnings per share of $4.50 and paid dividends per share of $2.00. Analysts expected both to grow 9.81% a year for the next 5 years. After the fifth year, the growth rate was expected to drop to 6% a year forever, while the payout ratio was expected to increase to 67.44%. The required return on Eli Lilly is 12.78%.
The price at the end of the high growth period can be estimated using the growing perpetuity formula:
Terminal price = DPS6 / (r - gn)
= EPS6 * Payout Ratio in Stable Growth / (r - gn)
= EPS0 (1+g)5 (1+gn) / (r - gn)
= $ 4.50*1.09815*1.06*0.6744/(.1278-.06) = $75.81
The present value of dividends and the terminal price can then be calculated as follows:
![]()
![]()
The value of Eli Lilly stock, based on the expected growth rates and discount rate, is $52.74.

The present value of these two annuities can be calculated separately and cumulated to arrive at the total present value. The present value of the second annuity has to be discounted back to the present.
Conclusion
Present value remains one of the simplest and most powerful techniques in finance, providing a wide range of applications in both personal and business decisions. Cash flow can be moved back to present value terms by discounting and moved forward by compounding. The discount rate at which the discounting and compounding are done reflect three factors: (1) the preference for current consumption, (2) expected inflation and (3) the uncertainty associated with the cash flows being discounted.