The FCFE Discount Model
WHY ARE DIVIDENDS DIFFERENT FROM FCFE?
- The FCFE is a measure of what a firm can afford to pay out as
dividends. Dividends paid are different from the FCFE for a number
of reasons --
- Desire for Stability
- Future Investment Needs
- Tax Factors
- Signalling Prerogatives
IV. THE CONSTANT GROWTH FCFE MODEL
The Model
The value of equity, under the constant growth model, is a function
of the expected FCFE in the next period, the stable growth rate
and the required rate of return.
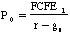
where,
P0= Value of stock today
FCFE1 = Expected FCFE next year
r = Cost of equity of the firm
gn= Growth rate in FCFE for the firm forever
This model is appropriate when
- The firm has to be in steady state. This also implies that.
(1) Capital expenditure is not significantly greater than depreciation.
(2) The beta of the stock is close to one or below one.
- The firm has FCFE which are significantly different from dividends,
or dividends are not relevant.
- The leverage is stable.
Illustration 7: FCFE Stable Growth Model: Telefonica de Espana
Rationale for using Model
- Given that the market that is serves (Spain) is reaching maturity
(40.5 phone lines per 100 people), and the regulations on local
pricing, it is unlikely that Telefon. Espana will be able to register
above-normal growth. It is expected to grow about 10% a year in
Spanish peseta terms.
- Telefonica pays out much less in dividends than it generates in
FCFE.
Dividends in 1995 = 54 Pt / share
FCFE per Share in 1995 = 86.53 Pt / share
Background Information
- Current Information:
- Earnings per Share = 154.53 Pt
- Capital Expenditures per share = 421 Pt
- Depreciation per share = 285 Pt
- Change in Working Capital / Share = None
- Debt Financing Ratio = 50%
- Earnings, Capital Expenditures and Depreciation are all expected
to grow 10% a year
- The beta for the stock is 0.90, and the Spanish long bond rate
is 9.50%. A premium of 6.50% is used for the Spanish market.
Valuation
- Cost of Equity = 9.50% + 0.90 (6.50%) = 15.35%
- Expected Growth Rate = 10.00%
- Base Year FCFE
Earnings per Share = 154.53
- (Capital Expenditures - Depreciation) (1 - Debt Ratio) = (421-285)(1-.5)
= - 68.00
- (Change in Working Capital) (1 - Debt Ratio) = 0 (1-.5) = -
0.00
= FCFE = 86.53
Value per Share = 86.53 (1.10)/ (.1535 - .10) = 1779 Pt
The stock was trading for 1788 Pt in January 1996.
Illustration 8: Valuing a firm with depressed earnings: Daimler
Benz
A rationale for using the FCFE Stable Model
- As one of the largest firms in a mature sector, it is unlikely
that Daimler Benz will be able to register super normal growth
over time.
- Like most German firms, the dividends paid bear no resemblance
to the cash flows generated.
- The leverage is stable and unlikely to change.
Background Information
- The company had a loss of 38.63 DM per share in 1995, partly because
of restructuring charges in aerospace and partly because of troubles
(hopefully temporary) at it automotive division.
- The book value of equity in 1995 was 20.25 billion DM.
- While the return on equity in 1995 period is negative, the five-year
average (1988-1993) return on equity is 10.17%.,
- The company reported capital expenditures of 10.35 billion DM
in 1995 and depreciation of 9.7 billion DM.
- The company has traditionally financed its investment needs with
35% debt and 65% equity.
- The working capital requirements are about 2.5% of revenues. The
revenues in 1995 is 104 billion DM.
- The stock had a beta of 1.10, relative to the Frankfurt DAX. The
German long bond rate is 6%. The risk premium for the German market
is 4.5%.
- In the long term, earnings are expected to grow at the same rate
as the world economy (6.5%).
- There are 51.30 million shares outstanding.
Valuation
Normalized Net Income = 20,250 * 0.1017 = 2059 million DM
- (Cap Ex - Deprecín) (1- Debt Ratio) = (10,350-9700) (1-.35)
= - 423 million DM
- Change in Working Capital (1 - Debt Ratio) = (.025 * .065* 104,000)
* 0.65
= - 110 million DM
= Free Cash Flows to Equity = 1526 million DM
- Cost of Equity = 6% + 1.10 (4.5%) = 10.95%
Value of Equity = 1526 million DM (1.065)/ (.1095 - .065) = 36,521
million DM
Value per Share = 36,521/51.30 = 712 DM
The stock was trading for 814 DM in February 1996.
V. THE TWO-STAGE FCFE MODEL
The Model
The value of any stock is the present value of the FCFE per year
for the extraordinary growth period plus the present value of
the terminal price at the end of the period.
Value = PV of FCFE + PV of terminal price
where,
FCFEt = Free Cashflow to Equity in year t
Pn= Price at the end of the extraordinary growth period
r = Required rate of return to equity investors in the firm
The terminal price is generally calculated using the infinite
growth rate model,
Pn= FCFEn+1 / (r - gn)
where,
gn= Growth rate after the terminal year forever.
Calculating the terminal price
- The same caveats that apply to the growth rate for the stable
growth rate model, described in the previous section, apply here
as well.
- In addition, the assumptions made to derive the free cashflow
to equity after the terminal year have to be consistent with this
assumption of stability. (Difference between capital expenditures
and depreciation will narrow; Beta closer to one)
Estimating Net Capital Expenditures in Steady State
There are three ways in which net capital expenditure is estimated
in steady state ñ
1. The Bludgeon Approach: Assume that capital expenditures offset depreciation, resulting
in a net cap ex of zero.
Limitations: If net cap ex is zero, where is real growth coming
from?
2. Industry Averages: Use industry average ratios of cap ex to depreciation to determine
the net cap ex in stable growth. (See Industry Average Table on
last page)
Limitations: Industry averages may themselves shift over time;
Firms may vary within the industry.
3. Firm-Specific Approach: Use the firmís characteristics to estimate what the net cap
ex will need to be in steady state. Based upon the increase in
earnings per share being estimated, and the return on equity earned
by the firm, the net cap ex can be estimated as follows:
Net Capital Expenditure per share in terminal year = (Increase
in $ EPS in terminal year)/ Estimated Return on Equity
Thus, if the earnings per share is projected to increase from
$ 2 to $ 2.12 in the terminal year, and the return on equity is
15%, the net capital expenditure per share in the terminal year
can be estimated as follows ñ
Net Capital Expenditure per share in terminal year = $ 0.12 /
.15 = $ 0.80
A similar analysis can be done in terms of after-tax operating
earnings and return on assets _
Net Capital Expenditures in terminal year = (Increase in EBIT(1-t)
in terminal year/ Estimated Return on Assets during stable growth.
Works best for:
- firms where growth will be high and constant in the initial period
and drop abruptly to stable growth after that.
- Dividends are very different from FCFE or not relevant / measurable
(private firms, IPOs)
- Firms which dont pay dividends but have negative FCFE.
Illustration 9: Two-Stage FCFE Model: Amgen Inc
A Rationale for using the Model
- Why two-stage? While Amgen has had a history of extraordinary growth, its growth
is moderating because ñ (a) it is becoming a much larger company
and (b) its products are maturing and may face competition soon.
- Why FCFE? Amgen does not pay dividends, but has some FCFE. This FCFE is
likely to increase as the growth rate moderates, and the firm
gets larger.
- Leverage is stable.
Background Information
- Current Earnings / Capital Expenditures
- Earnings per share in 1995 = $ 1.95
- Capital Expenditures in 1995 per share = $ 0.40
- Depreciation per share in 1995 = $0.32
- Revenues per share = $ 7.45
- Inputs for the High Growth Period
- Length of high growth period = 5 years
- Growth Rate inputs:
- Return on Equity = 21.74% (This is much lower than the current
return on equity of about 28%; This ROE is going to be difficult
to sustain as the firm gets larger)
- Retention Ratio = 100% (The firm pays no dividends now, and is
unlikely to do so in the near future because its stockholders
are more interested in price appreciation.
Expected Growth Rate = 1 * 21.74% = 21.74%
- The beta during the high growth phase is expected to be 1.30
Cost of Equity = 6.00% + 1.30 (5.50%) = 13.15%
- Capital expenditures, depreciation and revenues are expected to
grow at the same rate as earnings (21.74%)
- Working capital is expected to be 20% of revenues.
- The debt ratio is approximately 9.55%; it is expected to remain
unchanged.
- Inputs for the Stable Growth
- Expected Growth Rate = 6%
- Beta during stable growth phase = 1.10 : Cost of Equity = 6.00%
+ 1.1 (5.5%) = 12.05%
- Capital expenditures and depreciation are assumed to continue
growing 6% a year.
- Working capital is expected to be 20% of revenues.
- The debt ratio is expected to remain at 9.55%.
Estimating the value:
- The first component of value is the present value of the expected
FCFE during the high growth period.
|
1
|
2
|
3
|
4
|
5
|
|
| Earnings |
$2.37
|
$2.89
|
$3.52
|
$4.28
|
$5.21
|
|
| - (CapEx-Depreciation)*(1-_) |
$0.09
|
$0.11
|
$0.13
|
$0.16
|
$0.19
|
|
| -_ Working Capital*(1-_) |
|
$0.29
|
$0.36
|
$0.43
|
$0.53
|
$0.64
|
| Free Cashflow to Equity |
|
$1.99
|
$2.43
|
$2.95
|
$3.60
|
$4.38
|
|
Present Value @ 13.15%
|
$1.76
|
$1.89
|
$2.04
|
$2.19
|
$2.36
|
|
PV of FCFE during high growth phase = $1.76 + $1.89 + 2.04 + 2.19
+ 2.36 = $10.25
The price at the end of the high growth phase (end of year 5),
can be estimated using the constant growth model.
Terminal price = Expected FCFEn+1 / (r - gn)
Expected Earnings per share6 = 5.21 * 1.06 = $ 5.52
Expected FCFE6 = EPS6 - Net Capital Expenditures - D Working Capital (1 - Debt Ratio)
= $ 5.52 - $0.20 (1-.0955) - $ 0.24 (1-.0955) = $ 5.11
Terminal price = $ 5.11 /(.1205 -.06) = $ 84.39
The present value of the terminal price can be then written as
-
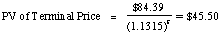
The cumulated present value of dividends and the terminal price
can then be calculated as follows:
PV today = PV of FCFE during high growth phase + PV of Terminal
Price = $10.25 + $45.50 = $55.75
Amgen was trading at $60.75 in February 1996, at the time of this
analysis.
VI. THE E-MODEL - A THREE STAGE FCFE MODEL
The Model
The E model calculates the present value of expected free cash
flow to equity over all three stages of growth:
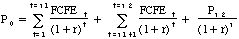
where,
P0= Value of the stock today
FCFEt = FCFE in year t
r = Cost of equity
Pn2 = Terminal price at the end of transitional period = FCFEn2+1/(r-gn)
n1 = End of initial high growth period
n2= End of transition period
Caveats in using model
1. Capital Spending versus Depreciation
- In the high growth phase, capital spending is likely to much larger
than depreciation. In the transitional phase, the difference is
likely to narrow and capital spending and depreciation should
be in rough parity in the stable growth phase.
2. Risk
- Over time, as these firms get larger and more diversified, the
average betas of these portfolios move towards one.
Works best for:
- firms with very high growth rates currently.
- firms whose dividends are significantly higher or lower than the
FCFE or dividends are not measurable
- firms with stable leverage
Illustration 10: Valuing America Online with the 3-stage FCFE
model
Rationale for using Three-Stage FCFE Model
- Why three stage? The expected growth rate in earnings is in excess of 50%, partly
because of the growth in the overall market and partly because
of the firmís position in the business.
- Why FCFE? The firm pays out no dividends, but has negative FCFE, largely
as a consequence of large capital expenditures.
- The firm uses little debt (about 10%) in meeting financing requirements,
and does not plan to change this in the near future.
Background Information
- Current Information
- Earnings per Share = $ 0.38
- Capital Spending per Share = $ 1.21
- Depreciation per Share = $ 0.17
- Revenues per share = $ 7.21
- Working Capital as a percent of revenues = 10.00% (This is significantly
lower than the current WC ratio)
- Phase 1: High Growth Period
- Length of the high growth period = 5 years
- Expected growth rate in earnings during the period = 52% (from
analyst projections and market growth)
- Capital Spending, depreciation and revenues will grow 20% a year
during this period (based upon past growth).
- Working capital will remain at 10% of revenues
- Approximately 10% of external financing will come from debt.
- The beta for the high growth period is 1.60.
- Phase 2: Transition period
- Length of the transition period = 5 years
- Growth rate will decline from 52% in year 5 to 6% in year 10 linearly.
- Capital Spending will grow 6% a year in this period, while depreciation
will continue to grow 12% a year.
- Revenues will increase 12% a year during this period; working
capital will remain 10% of revenues.
- The debt ratio will remain at 10% during this period
- The beta will decline linearly from 1.60 in year 5 to 1.20 in
year 10.
- Phase 3: Stable Growth Phase
- Earnings will grow 6% a year in perpetuity.
- Capital expenditures will be offset by depreciation.
- Revenues will also grow 6% a year; Working capital will remain
10% of revenues.
- The debt ratio will remain at 10% during this period.
- The beta for the stock will be 1.20
Valuing the Stock
The following are the expected cashflows over both periods.
|
Year
|
1
|
2
|
3
|
4
|
5
|
| High Growth Period |
|
|
|
|
|
| Earnings |
$0.58
|
$0.88
|
$1.33
|
$2.03
|
$3.08
|
| (CapEx-Depreciation)*(1-0.1) |
$1.12
|
$1.34
|
$1.61
|
$1.94
|
$2.32
|
| DWorking Capital *(1-0.1) |
$0.13
|
$0.16
|
$0.19
|
$0.22
|
$0.27
|
| FCFE |
($0.67)
|
($0.62)
|
($0.47)
|
($0.13)
|
$0.49
|
| Present Value |
($0.58)
|
($0.46)
|
($0.30)
|
($0.07)
|
$0.23
|
|
|
|
|
|
|
| Transition period |
|
|
|
|
|
| Year |
6
|
7
|
8
|
9
|
10
|
| Growth Rate |
42.80%
|
33.60%
|
24.40%
|
15.20%
|
6.00%
|
| Cumulated Growth |
42.80%
|
90.78%
|
137.33%
|
173.41%
|
189.81%
|
| Earnings |
$4.40
|
$5.88
|
$7.32
|
$8.43
|
$8.94
|
| (CapEx-Depreciation)*(1-0.1) |
$2.44
|
$2.56
|
$2.68
|
$2.81
|
$2.95
|
| DWorking Capital *(1-0.1) |
$0.19
|
$0.22
|
$0.24
|
$0.27
|
$0.30
|
| FCFE |
$1.77
|
$3.11
|
$4.39
|
$5.34
|
$5.69
|
| Beta |
1.52
|
1.44
|
1.36
|
1.28
|
1.2
|
| Cost of Equity |
15.86%
|
15.42%
|
14.98%
|
14.54%
|
14.10%
|
| Present Value |
$0.72
|
$1.09
|
$1.34
|
$1.43
|
$1.33
|
The free cashflow to equity in year 11, assuming that capital
expenditures are offset by depreciation, is $9.15, yielding a
terminal price of $ 112.94.
FCFE in year 11 = EPS11 - (Rev11-Rev10)*Working Capital as % of Revenues * (1- Debt Ratio)
= ($8.94*1.06) - $0.35 (1-.10) = $9.15
Cost of Equity in stable phase = 7.5% + 1.20 (5.50%) = 14.10%
Terminal price = $9.15 /(.1410-.06) = $112.94
The present value of free cashflows to equity and the terminal
price is as follows:
| Present Value of FCFE in high growth phase = |
($1.18)
|
| Present Value of FCFE in transition phase = |
$5.91
|
| Present Value of Terminal Price = |
|
$26.42
|
| Value of the stock = |
|
$31.15
|
America Online was trading at $86.75 in March 1995.
Emerging Market Illustration 11: Valuing Titan Watches (India)
with the 3-stage FCFE model
Rationale for using Three-Stage FCFE Model
- Why three stage? The expected growth rate in earnings is 35%, partly because the
overall market is huge (while 143 watches are purchased on average
per 1000 people worldwide, only 17 are sold per 1000 are sold
in India), and partly because of the companyís strong brand name.
- Why FCFE? The firm pays out a dividend, but the dividend has been fixed
at Rs 2.50 per share for three years. The free cash flows to equity
are much more volatile and have generally been negative in the
last few years.
- The firm uses little debt (about 10%) in meeting financing requirements,
and does not plan to change this in the near future.
Background Information
- Current Information
- Earnings per Share = Rs 6.20
- Capital Spending per Share = Rs 10.40
- Depreciation per Share = Rs 4.40
- Revenues per share = Rs 90.00
- Working Capital as a percent of revenues = 15.00%
- Phase 1: High Growth Period
- Length of the high growth period = 5 years
- Expected growth rate in earnings during the period = 35% (from
analyst projections and market growth)
- Capital Spending, depreciation and revenues will grow 30% a year
during this period (based upon past growth).
- Working capital will remain at 15% of revenues
- Approximately 10% of external financing will come from debt.
- The beta for the high growth period is 1.20.
- Phase 2: Transition period
- Length of the transition period = 5 years
- Growth rate in earnings will decline from 35% in year 5 to 12%
in year 10 linearly.
- Capital Spending will grow 10% a year in this period, while depreciation
will continue to grow 15% a year.
- Revenues will increase 15% a year during this period; working
capital will remain 15% of revenues.
- The debt ratio will remain at 10% during this period
- The beta will decline linearly from 1.20 in year 5 to 1.00 in
year 10.
- Phase 3: Stable Growth Phase
- Earnings will grow 12% a year in perpetuity.
- Capital expenditures will be offset by depreciation.
- Revenues will also grow 12% a year; Working capital will remain
15% of revenues.
- The debt ratio will remain at 10% during this period.
- The beta for the stock will be 1.00
The riskfree rate for the Indian market is 11%, and a 7.50% risk
premium is employed.
Valuing the Stock
The following are the expected cashflows over both periods.
|
Year
|
1
|
2
|
3
|
4
|
5
|
| High Growth Period ( 5 years) |
|
|
|
|
|
| Earnings |
Rs8.37
|
Rs11.30
|
Rs15.25
|
Rs20.59
|
Rs27.80
|
| - (CapEx-Depreciation)*(1-_) |
Rs7.02
|
Rs9.13
|
Rs11.86
|
Rs15.42
|
Rs20.05
|
| - Chg. Working Capital *(1-_) |
Rs3.65
|
Rs4.74
|
Rs6.16
|
Rs8.01
|
Rs10.41
|
| FCFE |
(Rs2.30)
|
(Rs2.57)
|
(Rs2.77)
|
(Rs2.84)
|
(Rs2.66)
|
| Present Value |
(Rs1.91)
|
(Rs1.78)
|
(Rs1.60)
|
(Rs1.37)
|
(Rs1.07)
|
|
|
|
|
|
|
| Transition period |
|
|
|
|
|
| Year |
6
|
7
|
8
|
9
|
10
|
| Growth Rate |
30.40%
|
25.80%
|
21.20%
|
16.60%
|
12.00%
|
| Cumulated Growth |
30.40%
|
64.04%
|
98.82%
|
131.82%
|
159.64%
|
| Earnings |
Rs36.25
|
Rs45.61
|
Rs55.27
|
Rs64.45
|
Rs72.18
|
| (CapEx-Depreciation)*(1-_) |
Rs21.32
|
Rs22.61
|
Rs23.89
|
Rs25.17
|
Rs26.40
|
| Chg. Working Capital *(1-_) |
Rs6.77
|
Rs7.78
|
Rs8.95
|
Rs10.29
|
Rs11.84
|
| FCFE |
Rs8.17
|
Rs15.22
|
Rs22.43
|
Rs28.99
|
Rs33.95
|
| Beta |
1.16
|
1.12
|
1.08
|
1.04
|
1
|
| Cost of Equity |
19.70%
|
19.40%
|
19.10%
|
18.80%
|
18.50%
|
| Present Value |
Rs2.74
|
Rs4.28
|
Rs5.30
|
Rs5.76
|
Rs5.69
|
The free cashflow to equity in year 11, assuming that capital
expenditures are offset by depreciation, is Rs 67.59, yielding
a terminal price of Rs 112.94.
FCFE in year 11 = EPS11 - (Rev11-Rev10)*Working Capital as % of Revenues * (1- Debt Ratio)
= (Rs. 72.18*1.12) - Rs. 14.73 (1-.10) = Rs 67.59
Cost of Equity in stable phase = 11%+ 1.00* (7.50%) = 18.50%
Terminal price = Rs 67.59 /(.185-.12) = Rs. 1039.85
The present value of free cashflows to equity and the terminal
price is as follows:
| Present Value of FCFE in high growth phase = |
(Rs7.73)
|
| Present Value of FCFE in transition phase = |
Rs23.77
|
| Present Value of Terminal Price = |
|
Rs174.39
|
| Value of the stock = |
|
Rs190.43
|
Titan Watches was trading at Rs 125 at the time of this analysis.
Estimation Issues for Emerging Market Companies
I. Estimating Risk Parameters
|
Option
|
Limitations
|
1. Estimate the beta(s) by regressing returns on the stock against
returns on the market index.
Eg. Regress returns on Titan against Bombay Stock Exchange |
- Stock might not have been listed long
- Estimates might be very noisy
|
2. Estimate the beta(s) by sector, rather than by company, within
the local market.
Eg. Estimate the betas for watch/electronic companies, and take
the average across the sector. |
- Might not be many firms in the sector.
- Too many differences across firms in each sector.
|
3. Use the beta from another market for a similar company.
Eg. Use the beta of a U.S. company or companies manufacturing
watches. |
- Risk levels might be different across countries because of differences
in operating and regulatory risk.
|
4. Use accounting earnings to estimate betas instead of market
prices.
Eg. Run a regression of Titan earnings against overall earnings. |
- Accounting earnings may be even more volatile than stock prices.
- There might not be a long enough history.
|
5. Use subjective risk measures - classify firms into risk classes
and calculate expected returns by risk class.
Eg. Classify Titan as high, average or low risk, and demand appropriate
returns. |
- Subjective judgment might be erroneous.
- This approach mixes firm-specific and market risk.
|
| 6. Make no risk adjustment. All firms have the same required rate
of return. |
- Will be disastrous if firms are of very different risk classes.
|
II. Estimating Cash Flows
- There is not much historical data.
- The data is unreliable.
- The company and the economy are changing too fast.
While all these factors increase the uncertainty associated with
the estimates, this noise is partially the result of poor information
and partially the result of
FCFE Valuation versus Dividend Discount Model Valuation
a. When they are similar
- where the dividends are equal to the FCFE.
- where the FCFE is greater than dividends, but the excess cash
is invested in projects with net present value of zero.
b. When they are different
- when the FCFE is greater than the dividend and the excess cash
either earns below-market interest rates or is invested in negative
net present value projects
- the payment of smaller dividends than can be afforded to be paid
out by a firm, lowers debt-equity ratios and may lead the firm
to become underleveraged, causing a loss in value.
- In the cases where dividends are greater than FCFE, the firm will
have to issue either new stock or new debt to pay these dividends
leading to at least three negative consequences for value.
- One is the flotation cost on these security issue
