Value of Zero Coupon Bond =![]()
An investor, having decided on the proportions of the portfolio that he or she would like to invest in stocks, bonds and real assets, has to decide on exactly what stocks he or she will hold in the stock portion of the portfolio, what bonds in the bond portion and what real assets in the real asset portion. This asset selection decision, like the asset allocation decision, can be an active one, where the investor attempts to buy undervalued assets in each asset class (or sell overvalued ones) or a passive one, where the investor invests across assets in an asset class, without attempting to make judgments on under or over valuation. In this chapter, we will examine not only this fundamental choice but also a whole range of active asset selection strategies and the evidence on whether they, in fact, deliver superior returns. We will also examine the case for passive asset selection.
It is every investor’s fervent hope to "beat the market" and active asset selection plays to this hope. As attested to by the success of investment newsletters and investment advice books, there are hundreds of investment strategies that investors use to select what they hope will be the best-performing assets in any asset class. Active asset selection strategies can be classified fairly broadly into four classes - intrinsic valuation models that use financial information on an asset in valuation models to find out whether the asset is under or over valued, relative valuation models that attempt to find assets that are undervalued relative to comparable assets or use investment screens to accomplish the same purpose, technical analysis models that use price and volume information on assets to detect trends in prices and private information models that attempt to get more or better information on an asset than is available to other investors in the asset.
1. Intrinsic Valuation Models
In intrinsic valuation, the value of any asset is viewed as a function of the cash flows generated by that asset, the life of the asset, the expected growth in the cash flows and the riskiness associated with the cash flows. Building on one of the first principles in finance, the value of an asset can be viewed as the present value of the expected cash flows on that asset.
A. Basics of Intrinsic Valuation
There are three inputs that are required to value any asset in this model - the expected cash flow, the timing of the cash flow and the discount rate that is appropriate given the riskiness of these cash flows.
At the most general level, the cash flow on an investment can either be a residual cash flow on that investment left over after other claim holders (such as debt used to finance the asset) have been paid off, in which case it is called a cash flow to equity, or a cumulative cash flow to all claim holders in the asset, in which case it is called a cash flow to the firm. The discount rate should be defined consistently. If the cash flows are only to the equity investors, it is the rate that equity investors would need to make given the risk in the investment, which is the cost of equity. Clearly, riskier equity investors should lead to higher costs of equity. If the cash flows are to all claimholders, the discount rate has to be an average of the rates demanded by all of the claimholders, weighted by the proportion of the value held by each; this is the cost of capital.
B. The Continuum of Risk
The model is generic enough to apply to any kind of asset. The simplest asset that we can think of from a valuation perspective is a default-free zero-coupon bond, which has only one cash flow that occurs at maturity and a discount rate that is the riskless rate corresponding to that maturity. The value of this bond can be written as the present value of a single cash flow discounted back at the riskless rate.
Value of Zero Coupon Bond =![]()
where r is the market interest rate on the zero-coupon and t is the maturity of the zero-coupon bond. Since the cash flow on this bond is fixed, the value of this bond will vary inversely with the discount rate.
One step up the chain of complexity is a default-free coupon bond, which has fixed cash flows (coupons) that occur at regular intervals (say semi annually) and a final cash flow (face value) at maturity. This bond can be viewed as a collection of zero coupon bonds and each can be valued using the riskless rate that corresponds to when the cash flow comes due:
![]()
where rt is the interest rate that corresponds to a t-period zero coupon bond and the bond has a life of N periods. It is, of course, possible to arrive at the same value using some weighted average of the year-specific riskless rates used above. This rate is called the yield to maturity:
![]()
where r is the yield to maturity on the bond. As with the zero-coupon bond, the default-free coupon bond should have a value that varies inversely with the yield to maturity. Since the coupon bond has cash flows that occur earlier in time (the coupons) it should be less sensitive to a given change in interest rates than the zero-coupon bond.
The next step in terms of risk is default risk, which exists when entities other than the government issue securities. While the basic structure of the valuation remains the same, i.e., expected cash flows are discounted at a discount rate; the discount rate used for a bond with default risk will be higher than that used for default-free bond. Furthermore, as the default risk increases, so will the discount rate used:
![]()
where rc is the market interest rate on bonds with similar default risk. (This analysis can be done in terms of year-specific zero-coupon rates as with the government bond.) The default risk of borrowing entities is often measured by independent agencies that assign bond ratings that attempt to measure this risk. To the degree that these ratings are accurate, bonds in the same ratings class should be priced to yield the same rate of return. Since the ratings are discrete and agencies sometimes lag the markets, it is common in financial markets to see bonds with the same ratings priced to yield slightly different returns.
In a corporate bond the cash flows are promised, but the risk comes from the fact that these cash flows might not be delivered. In equity investments, the cash flows are residual cash flows and the risk arises from the volatility of these expected cash flows. In the continuum of risk, these investments should be riskier than bonds issued by the same entities because the priority of claims favors the bond holders. The value of an equity investment follows the same discounted cash flow principles, however. Thus, the value of the equity investment in an asset with a fixed life of N years, say an office building, can be written as follows:
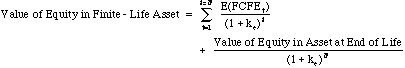
where E(FCFEt) is the expected cash flow to equity investors after making debt payments in period t, ke is the rate of return that the equity investor in this asset would demand given the riskiness of the cash flows and the value of equity at the end of the asset’s life is the value of the asset net of the debt outstanding on it. The value of the entire asset and not just the equity in it can also be similarly estimated using the cumulated cash flows to all claim holders on the assets (cash flow to the firm) and discounting at the weighted average of their required rates of return (cost of capital).
![]()
where E(FCFFt) is the expected cash flow on the asset prior to payments to any of the claim holders and kc is the cost of capital. Note, however, that the value of the equity can be obtained from this by subtracting out the value of the non-equity claims (such as debt).
Equity investments in entities with infinite lives can be assessed similarly as the present value of the cash flows over the perpetuity.
![]()
Practically speaking, cash flows cannot be estimated forever, but valuation models draw on a present value relationship that proves useful in getting closure in these models. The present value of a cash flow growing at a constant rate forever can be written in terms of the expected cash flow next period, the discount rate and the expected growth rate:
![]()
where CF1 is the cash flow one period from now, r is the discount rate and g is the growth rate forever. Thus, the value of the equity investment in a firm growing at a constant rate forever (called a stable growth rate) can be assessed using this model.
![]()
where gn is the expected growth rate in cash flows to equity forever. Note that since the growth rate has to be sustainable forever, it cannot exceed the growth rate of the economy in which the firm operates, and this constraint will always ensure that the growth rate will be less than the cost of equity (which has incorporated into it a riskless rate). Similarly, the value of the asset (rather than just the equity in it) can be estimated using the same approach:
![]()
where gn is the growth rate in cash flows to the asset forever. In the more general framework, where the asset is a business which may be growing at a rate far greater than the stable growth rate currently, the model described above is used to get the terminal value at the end of the period of high growth.
![]()
where the high growth is expected to last N periods, and the terminal value of equity at the end of N periods is estimated using the constant-growth model described above. The value of the entire business can be estimated as well:
![]()
The approach is general enough to apply to all firms ranging from stable firms with large earnings and cash flows to high-growth firms, which might have negative cash flows currently but are expected to have positive cash flows in the future, to troubled firms, which may be losing money currently but are expected to turn around in the future.
C. Inputs to Valuation
In this section we will examine in a little more detail the process by which we estimate the inputs to discounted cash flow models - the cash flows themselves, the growth rate in these cash flows and the discount rate.
1. Cash Flows
There are two basic cash flows that investors can choose to discount - cash flows to equity investments or cash flows to the firm. In the strictest sense, the only cash flow an equity investor gets out of a publicly traded firm is the dividend; models that use the dividends as cash flows are called dividend discount models. A broader definition of cash flows to equity would be the cash flows left over after the cash flow claims of non-equity investors in the firm have been met (interest and principal payments to debt holders and preferred dividends) and after enough of these cash flows has been reinvested enough of the cash flows back into the firm to sustain the projected growth in cash flows. This is called the free cash flow to equity (FCFE), and models that use these cash flows are called FCFE discount models.
Illustration 1: Estimating Free Cash Flow to Equity for a firm: General Electric
General Electric reported net income of $6,777 million in 1995. In the same year, it had capital expenditures of $ 6,447 million and depreciation of $3,594 million. Non-cash working capital increased by $ 125 million during the year to $ 1.5 billion at year-end. At the end of the year, the market value of equity at GE, obtained by multiplying the number of shares outstanding (1651 million) by the share price ($92.375), was $152 billion. GE also had debt outstanding of $ 115 billion. Analysts were estimating that earnings would grow 10% in 1996. If we assume that capital expenditure, depreciation and working capital all grow at the same rate as earnings, and that GE maintains its market value debt ratio at 1995 levels, the free cash flow to equity in 1996 can be estimated as follows:
|
|
|
|
|
Net Income
|
|
|
|
- (Net Capital Expenditures) (1- Debt Ratio)
|
|
|
|
- (Change in Working Capital) (1- Debt Ratio)
|
|
|
|
Free Cashflow to Equity
|
|
|
|
Information Used
|
||
|
Net Capital Expenditures
|
$ 2,853
|
$ 3,138
|
|
Change in Working Capital
|
$ 125
|
$ 150
|
|
Debt Ratio
|
43.07%
|
43.07%
|
The difference between capital expenditures and depreciation is referred to as net capital expenditures. When added on to the change in non-cash working capital, it provides a measure of how much GE has to reinvest back to create future growth. We look at only the equity portion of this investment by netting out the debt portion.
The cash flow to the firm is the cumulated cash flow to all claimholders in the firm. One way to obtain is to add the free cash flows to equity to the cash flows to debt and preferred stock. A far simpler way of obtaining the same number is to estimate the cash flows prior to debt payments, by subtracting from the after-tax operating income the net investment needs to sustain growth. This cash flow is called the free cash flow to the firm (FCFF) and the models that use these cash flows are called FCFF models.
Illustration 2: Estimating Free Cash Flow to Firm - General Electric
Consider the example of General Electric, for which we estimated free cashflows to equity in 1996. A similar estimate can be made of cash flows to the firm, with the same inputs as those used for the free cash flows to equity. The additional information that is provided is that GE had earnings before interest and taxes of $ 16.339 billion in 1995 and expected these earnings to grow 10% in 1996. The free cashflow to the firm can then be estimated as follows:
|
|
|
|
|
EBIT (1- Tax Rate)
|
|
|
|
- Net Capital Expenditures
|
|
|
|
- Change in Working Capital
|
|
|
|
Free Cashflow to Firm
|
|
|
|
Information Used
|
||
|
Tax Rate
|
|
|
|
Net Capital Expenditures
|
|
|
|
Change in Working Capital
|
|
|
Note, unlike the free cash flow to equity, that it is the entire net capital expenditures and working capital change that is subtracted from after-tax operating income to arrive at the free cash flow to the firm.
2. Expected Growth
While the expected growth rate is an input in most valuation models, it is itself an output of two variables that are determined by the firm being valued - how much of the earnings are reinvested back into the firm and how well those are earnings are reinvested. In the equity valuation model, this expected growth rate is a product of the retention ratio , i.e. the proportion of net income not paid out to stockholders, and the return on equity on the projects taken with that money. In the firm valuation model, the expected growth rate is a product of the reinvestment rate, which is the proportion of after-tax operating income that goes into net new investments and the return on capital earned on these investments.
Illustration 3: Estimating Expected Growth in EPS and after-tax Operating Income for GE
The expected growth in Earnings per share at GE can be estimated using the retention ratio (that measures the percentage of net income that is reinvested back in the company) and the expected return on equity. If we assume that the 1995 estimates for these numbers hold, then
Retention Ratio = 58%
Return on Equity = 23.4%
Expected Growth Rate in Earnings per Share = (0.58) (0.234) = 13.57%
The expected growth rate in operating income is a little more involved. It requires an estimation of the reinvestment rate, which in 1995 was:
Reinvestment Rate = (Net Capital Expenditures + Change in WC)/ EBIT (1-t)
= (2853+125)/10,457 = 28.48%
Return on Capital = EBIT (1-t)/ Average BV of Capital = 10,457/83,408 = 12.54%
Expected Growth Rate in Operating Income = (.2848) (12.54%) = 3.57%
It is leverage that allows the growth rate in earnings per share to be so much greater than the growth rate in operating income. We are implicitly assuming that the current returns on book value of equity and capital are good measures of what GE will make in the future. To the degree that this is not true, estimates of returns on equity and capital on future projects have to be used instead.
3. Discount Rates
Earlier in this book, we were introduced to a number of risk and return models. While these models, such as the capital asset pricing model (CAPM) and the arbitrage pricing model (APM), look different in their final forms and arrive there making different assumptions, they agree on some fundamental principles. First, the risk in an investment that should drive discount rates is the non-diversifiable or market risk. In the CAPM, this market risk is measured using the beta of the asset relative to a portfolio that includes all traded assets in that market (or the market portfolio). In the APM, the market risk is measured relative to multiple macro economic factors with each asset having a beta relative to each factor. Second, the average of the beta(s) in the CAPM (APM) across all assets is one. Third, the expected return on any investment can be obtained by adding to the riskless rate the product of the beta and the risk premium on the market portfolio in the CAPM, and the sum of the products of the betas and the risk premium relative to each macro economic factors in the APM. This expected return, for an equity investment, is the cost of equity.
The cost of capital can be obtained by taking an average of the cost of equity, estimated as above, and the after-tax cost of borrowing, weighted by their market value. While there are some who use book value weights, doing so violates a basic principle of valuation, which is that at a fair value, one should be indifferent between buying and selling.
Illustration 3: Estimating Costs of Equity and Capital: GE
In 1995, GE’s equity had a beta of 1.15 and its debt was AAA rated. Given the long term government bond rate of 7% at that time, the cost of equity and the cost of capital can be estimated as follows. The cost of equity is estimated using the long term bond rate, the beta and a risk premium for stocks over bonds of 5.5% based upon historical data:
Cost of Equity = 7% + 1.15 (5.5%) = 13.33%
The cost of debt is obtained by adding a default premium of 0.30% to the long term government bond rate, based upon the AAA rating, and adjusting for the tax benefits of debt based upon the marginal corporate tax rate of 36%.
After-tax Cost of Debt = 7.30% (1-.36) = 4.67%
Finally the market values of debt and equity are obtained:
Market Value of Equity = 1651 million shares * $92.375 = $ 152 billion
Market Value of Debt = $ 115 billion
Cost of Capital = 13.33% (152/(152+115)) + 4.67% (115/(115+152)) = 9.60%
(As a contrast, the book value of equity was only $ 32 billion, which would have yielded a cost of capital of around 7.5%)
D. Limitations of DCF Valuation
There are several reasons portfolio managers may desist from using discounted cash flow valuation. First, discounted cash flow valuation is the most information intensive of the valuation approaches we will cover in this section. This may make it unsuitable for portfolio managers who have to pick from large universes of assets. Second, it requires inputs many years into the future. The inherent uncertainty in these estimates leads some to conclude that valuation is not a particularly productive exercise. I would argue otherwise. Not doing a discounted cash flow valuation does not make the uncertainty go away; it just sweeps it under the carpet. Third, discounted cash flow valuation is also likely to reveal the analysts’ biases. Since the value can be moved around by changing one of two inputs in the process, it is not unusual to see valuations change to reflect the strong prior view that the analyst might have. Here again, I would argue that discounted cash flow valuation is not unique. All valuation approaches will be colored by the analysts’ biases. In fact, by forcing analysts to be explicit with their assumptions, discounted cash flow valuation may be more successful than other approaches in revealing these biases to outsiders.
E. Usage and Empirical Evidence
The usage of discounted cash flow models among portfolio managers seems to be fairly limited. A survey in the Journal of Portfolio Management reported that less than 20% of portfolio managers used discounted cash flow valuation as their primary tool for picking undervalued assets. One reason for this may be the difficulty of applying time and information intensive valuation techniques on large universes of stocks. Another may be the failure of the model to consider market moods and perceptions, which some contrarians may view as a strength, but which may still lead the analyst to find all stocks in some sectors to be over valued. For a portfolio manager who has to be invested in equities, this may not be a practical solution. Finally, investment success with discounted cash flow valuation requires not only skill at valuation but also that other investors come to the same realization and adjust the price towards the value. If the analysts’ predictions of earnings and cash flows are on the mark, this will happen eventually, but it might not happen anytime in the near future. Portfolio managers who are often evaluated on a short-term basis may not have the luxury of time as an ally.
There have been relatively few studies that have examined whether asset selection using discounted cash flow valuation yields excess returns. Part of the reason for the paucity of studies is that testing the proposition that DCF valuation pays off requires that large numbers of assets be valued using discounted cash flow valuation at points in time and the excess returns in the following periods be correlated with these valuations. One study in the Financial Analysts Journal noted that using the dividend discount model allowed investors to earn excess returns, but the stocks that emerged as undervalued in these models tended to be stocks with low price-earnings ratios and high dividend yields, which, as we will see in the next section, are correlated with excess returns themselves.
II. Relative Valuation
In intrinsic valuation the objective is to find assets that are priced below what they should be, given their cash flow, growth and risk characteristics. In relative valuation, the philosophical focus is on finding assets that are cheap or expensive relative to how "similar" assets are being priced by the market right now. It is therefore entirely possible that an asset that is expensive on an intrinsic value basis may be cheap on a relative basis.
A. Standardized Values and Multiples
To compare the valuations of "similar" assets in the market, we need to standardize the values in some way. They can be standardized relative to the earnings that they generate, the book value or replacement value of the assets themselves or relative to the revenues that they generate. Each approach is used widely and has strong adherents.
1. Earnings Multiples
One of the more intuitive ways to think of the value of any asset is as a multiple of the earnings generated by it. When buying a stock, it is common to look at the price paid as a multiple of the earnings per share generated by the company. This price/earnings ratio can be estimated using current earnings per share (which is called a trailing PE) or a expected earnings per share in the next year (called a forward PE). When buying a business (as opposed to just the equity in the business) it is common to examine the value of the business as a multiple of the operating income (or EBIT) or the operating cash flow (EBITDA). While a lower multiple is better than a higher one, these multiples will be affected by the growth potential and risk of the business being acquired.
2. Book Value or Replacement Value Multiples
While markets provide one estimate of the value of a business, accountants often provide a very different estimate of the same business in their books. This latter estimate, which is the book value, is driven by accounting rules and are heavily influenced by what was paid originally for the asset and any accounting adjustments (such as depreciation) made since. Investors often look at the relationship between the price they pay for a stock and the book value of equity (or net worth) as a measure of how over or undervalued a stock it; the price/book value ratio that emerges can vary widely across sectors, depending again upon the growth potential and the quality of the investments in each. When valuing businesses, this ratio is estimated using the value of the firm and the book value of all assets (rather than just the equity). For those who believe that book value is not a good measure of the true value of the assets, an alternative is to use the replacement cost of the assets; the ratio of the value of the firm to replacement cost is called Tobin’s Q.
3. Revenue Multiples
Both earnings and book value are accounting measures and are affected by accounting rules and principles. An alternative approach, which is far less affected by these factors, is to look at the relationship between value of an asset and the revenues it generates. For equity investors, this ratio is the price/sales ratio, where the market value per share is divided by the revenues generated per share. For firm value, this ratio can be modified as the value/sales ratio, where the numerator becomes the total value of the firm. This ratio, again, varies widely across sectors, largely as a function of the profit margins in each. The advantage of these multiples, however, is that it becomes far easier to compare firms in different markets, with different accounting systems at work.
B. The Fundamentals Behind Multiples
One reason commonly given for relative valuation is that it requires far fewer assumptions than does discounted cash flow valuation. In my view, this is a misconception. The difference between discounted cash flow valuation and relative valuation is that the assumptions that an analyst makes have to be made explicit in the former and they can remain implicit in the latter. It is important that we know what the variables are that drive multiples, since these are the variables we have to control for when comparing these multiples across firms.
To look under the hood, so to speak, of equity and firm value multiples, we will go back to fairly simple discounted cash flow models for equity and firm value and use them to derive our multiples. Thus, the simplest discounted cash flow model for equity which is a stable growth dividend discount model would suggest that the value of equity is:
Value of Equity = ![]()
where DPS1 is the expected dividend in the next year, ke is the cost of equity and gn is the expected stable growth rate. Dividing both sides by the earnings, we obtain the discounted cash flow model for the PE ratio for a stable growth firm:
![]()
Dividing both sides by the book value of equity, we can estimate the Price/Book Value ratio for a stable growth firm:
![]()
where ROE is the return on equity. Dividing by the Sales per share, the price/sales ratio for a stable growth firm can be estimated as a function of its profit margin, payout ratio, profit margin and expected growth.
![]()
We can do a similar analysis from the perspective of firm valuation. The value of a firm in stable growth can be written as:
Value of Firm = ![]()
Dividing both sides by the expected free cash flow to the firm yields the Value/FCFF multiple for a stable growth firm:
![]()
Since the free cash flow the firm is the after-tax operating income netted against the net capital expenditures and working capital needs of the firm, the multiples of EBIT, after-tax EBIT and EBITDA can also be similarly estimated. The value/EBITDA multiple, for instance, can be written as follows:
![]()
The point of this analysis is not to suggest that we go back to using discounted cash flow valuation but to get a sense of the variables that may cause these multiples to vary across firms in the same sector. An analyst who is blind to these variables might conclude that a stock with a PE of 8 is cheaper than one with a PE of 12, when the true reason may by that the latter has higher expected growth, or that a stock with a P/BV ratio of 0.7 is cheaper than one with a P/BV ratio of 1.5, when the true reason may be that the latter has a much higher return on equity. The following table lists out the multiples that are widely used and the variables driving each; the variable, which in my view, is the most significant is highlighted for each multiple. This is what I would call the companion variable for this multiple, i.e., the one variable I would need to know in order to use this multiple to find under or over valued assets.
Table 1: Multiples and Companion Variables
Companion variables are in bold type
|
Multiple
|
Determining Variables
|
|
Price/Earnings Ratio
|
Growth, Payout, Risk
|
|
Price/Book Value Ratio
|
Growth, Payout, Risk, ROE
|
|
Price/Sales Ratio
|
Growth, Payout, Risk, Net Margin
|
|
Value/EBIT
Value/EBIT (1-t) Value/EBITDA |
Growth, Net Capital Expenditure needs, Leverage, Risk
|
|
Value/Sales
|
Growth, Net Capital Expenditure needs, Leverage, Risk, Operating Margin
|
|
Value/Book Capital
|
Growth, Leverage, Risk and ROC
|
C. The Use of Comparables
Most analysts who use multiples use them in conjunction with "comparable" firms to form conclusions about whether firms are fairly valued or not. At the risk of being simplistic, the analysis begins with two decisions - the multiple that will be used in the analysis and the group of firms that will comprise the comparable firms. The multiple is computed for each of the comparable firms, and the average is computed. To evaluate an individual firm, the analyst then compares its multiple to the average computed; if it is significantly different, the analyst makes a subjective judgment on whether the firm’s individual characteristics (growth, risk ..) may explain the difference. Thus, a firm may have a PE ratio of 22 in a sector where the average PE is only 15, but the analyst may conclude that this difference can be justified by the fact that the firm has higher growth potential than the average firm in the sector. If, in the analysts’ judgment, the difference on the multiple cannot be explained by the fundamentals, the firm will be viewed as over valued (if its multiple is higher than the average) or undervalued (if its multiple is lower than the average).
1. Choosing Comparables
The heart of this process is the selection of the firms that comprise comparable firms. From a valuation perspective, a comparable firm is one with similar cash flows, growth potential and risk. If life were simple, the value of a firm would be analyzed by looking at how an exactly identical firm - in terms of risk, growth and cash flows - is priced. In most analyses, however, a comparable firm is defined to be one in the same business as the firm being analyzed. If there are enough firms in the sector to allow for it, this list will be pruned further using other criteria; for instance, only firms of similar size may be considered. Implicitly, the assumption being made here is that firms in the same sector have similar risk, growth and cash flow profiles and therefore can be compared with much more legitimacy. This approach becomes more difficult to apply under two conditions:
1. There are relatively few firms in a sector. In most markets outside the United States, the number of publicly traded firms in a particular sector, especially if it is defined narrowly, is small.
2. The differences on risk, growth and cash flow profiles across firms within a sector is large. Thus, there may be hundreds of computer software companies listed in the United States, but the differences across these firms are also large.
The tradeoff is therefore a simple one. Defining a sector more broadly increases the number of firms that enter the comparable firm list, but it also results in a more diverse group.
2. Controlling for Differences across Firms
Since it is impossible to find identical firms to the one being valued, we have to find ways of controlling for differences across firms on the relevant ways. The advantage of the discounted cash flow models introduced in the prior section is that we have a clear idea of what the fundamental determinants of each multiple are, and therefore what we should be controlling for; table 1 provides a summary of the variables. The process of controlling for the variables can range from very simple approaches, which modify the multiples to take into account differences on one key variable, to more complex approaches that allow for differences on more than one variable.
Let us start with the simple approaches. Here, the basic multiple is modified to take into account the most important variable determining that multiple. Thus, the PE ratio is divided by the expected growth rate in EPS for a company to come up with a growth-adjusted PE ratio. Similarly, the PBV ratio is divided by the ROE to come up with a value ratio, and the price sales ratio by the net margin. These modified ratios are then compared across companies in a sector. Implicitly, the assumption made is that these firms are comparable on all the other dimensions of value, besides the one being controlled for.
Illustration 4: Comparing PE ratios and growth rates across firms: Software companies
In the following table, we have listed the PE ratios and expected analyst consensus growth rates over 5 years for a selected list of software companies:
| Company |
|
|
|
| Acclaim Entertainment |
|
|
|
| Activision |
|
|
|
| Broderbund |
|
|
|
| Davidson Associates |
|
|
|
| Edmark |
|
|
|
| Electronic Arts |
|
|
|
| The Learning Co. |
|
|
|
| Maxis |
|
|
|
| Minnesota Educational |
|
|
|
| Sierra On-Line |
|
|
|
While comparisons on the PE ratio alone do not factor in the differences in expected growth, the PEG ratio in the last column can be viewed as growth adjusted PE ratio and that would suggest that Acclaim is the cheapest company in this group and Minnesota Educational is the most expensive. This conclusion holds only if these firms are of equivalent risk, however.
When firms vary on more than one dimension, it becomes difficult to modify the multiples to take into account the differences across firms. It is, however, feasible to run regressions of the multiples against the variables and then use these regressions to get predicted values for each firm. This approach works reasonably well when the number of comparable firms is large and the relationship between the multiple and variable is strong. When these conditions do not hold, a few outliers can cause the coefficients to change dramatically and make the predictions much less reliable.
Illustration 5: PBV Ratios and ROE: The Oil Sector
The following table summarizes Price/Book Value ratios of oil companies and reports on their returns on equity and expected growth rates:
|
|
|
|
|
|
Total ADR B
|
0.90
|
4.10
|
9.50%
|
|
Giant Industries
|
1.10
|
7.20
|
7.81%
|
|
Royal Dutch Petroleum ADR
|
1.10
|
12.30
|
5.50%
|
|
Tesoro Petroleum
|
1.10
|
5.20
|
8.00%
|
|
Petrobras
|
1.15
|
3.37
|
15%
|
|
YPF ADR
|
1.60
|
13.40
|
12.50%
|
|
Ashland
|
1.70
|
10.60
|
7%
|
|
Quaker State
|
1.70
|
4.40
|
17%
|
|
Coastal
|
1.80
|
9.40
|
12%
|
|
Elf Aquitaine ADR
|
1.90
|
6.20
|
12%
|
|
Holly
|
2.00
|
20.00
|
4%
|
|
Ultramar Diamond Shamrock
|
2.00
|
9.90
|
8%
|
|
Witco
|
2.00
|
10.40
|
14%
|
|
World Fuel Services
|
2.00
|
17.20
|
10%
|
|
Elcor
|
2.10
|
10.10
|
15%
|
|
Imperial Oil
|
2.20
|
8.60
|
16%
|
|
Repsol ADR
|
2.20
|
17.40
|
14%
|
|
Shell Transport & Trading ADR
|
2.40
|
10.50
|
10%
|
|
Amoco
|
2.60
|
17.30
|
6%
|
|
Phillips Petroleum
|
2.60
|
14.70
|
7.50%
|
|
ENI SpA ADR
|
2.80
|
18.30
|
10%
|
|
Mapco
|
2.80
|
16.20
|
12%
|
|
Texaco
|
2.90
|
15.70
|
12.50%
|
|
British Petroleum ADR
|
3.20
|
19.60
|
8%
|
|
Tosco
|
3.50
|
13.70
|
14%
|
Since these firms differ on both growth and return on equity, we ran a regression of PBV ratios on both variables:
PBV = -0.11 + 11.22 (ROE) + 7.87 (Expected Growth) R2 = 60.88%
(5.79) (2.83)
The numbers in brackets are t-statistics and suggest that the relationship between PBV ratios and both variables in the regression are statistically significant. The R-squared indicates the percentage of the differences in PBV ratios that is explained by the independent variables. Finally, the regression itself can be used to get predicted PBV ratios for the companies in the list. Thus, the predicted PBV ratio for Repsol would be:
Predicted PBVRepsol = -0.11 + 11.22 (.1740) + 7.87 (.14) = 2.94
Since the actual PBV ratio for Repsol was 2.20, this would suggest that the stock was undervalued by roughly 25%.
Both approaches described above assume that the relationship between a multiple and the variables driving value are linear. Since this is not necessarily true, it is possible to run non-linear versions of these regressions.
3. Expanding the Comparable Firm Universe
Searching for comparable firms within the sector in which a firm operates is fairly restrictive, especially when there are relatively few firms in the sector or when a firm operates in more than one sector. Since the definition of a comparable firm is not one that is in the same business but one that has the same growth, risk and cash flow characteristics as the firm being analyzed, it is also unclear why we have to stay sector-specific. A software firm should be comparable to an automobile firm, if we can control for differences in the fundamentals.
The regression approach that we introduced in the previous section allows us to control for differences on those variables that we believe cause differences in multiples across firms. Using the minimalist version of the regression equations here, we should be able to regress PE, PBV and PS ratios against the variables that should affect them:
PE = a + b (Growth) + c (Payout ratios) + d (Risk)
PBV = a + b (Growth) + c (Payout ratios) + d (Risk) + e (ROE)
PS = a + b (Growth) + c (Payout ratios) + d (Risk) + e (Margin)
It is, however, possible that the proxies that we use for risk (beta) , growth (expected growth rate) and cash flow (payout) may be imperfect and that the relationship may not be linear. To deal with these limitations, we can add more variables to the regression - e.g., the size of the firm may operate as a good proxy for risk - and use transformations of the variables to allow for non-linear relationships.
We ran these regressions for PE, PBV and PS ratios across publicly listed firms in the United States in March 1997 twice - once with individual firms as our observations and once with the firms aggregated into sectors (which reduces the noise in the estimates). The sample, which had 4527 firms in it, yielded the regressions reported in Table 2. These regressions can then be used to get predicted PE, PBV and PS ratios for each firm, which, in turn, can be compared to the actual multiples to find under and over valued firms.
Put Table 2 here
The first advantage of this approach over the "subjective" comparison across firms in the same sector described in the previous section is that it does quantify, based upon actual market data, the degree to which higher growth or risk should affect the multiples. It is true that these estimate can be noisy, but this noise is a reflection of the reality that many analysts choose not to face when they make subjective judgments. Second, by looking at all firms in the universe, it allows analysts operating in sectors with relatively few firms in them to make more powerful comparisons. Finally, it gets analysts past the tunnel vision induced by comparing firms within a sector, when the entire sector may be under or over valued.
D. Screening for Value
Investors have used multiples of one kind or another to find misvalued assets in markets for as long as they have been investing. Portfolio managers, who have to pick from very large universes of assets, often use simple screens to prune the universe down to a manageable portfolio. For instance, a portfolio manager may screen 4500 stocks for those with PE ratios less than 12, market capitalization less than $ 2 billion and institutional holdings less than 25% to arrive at a portfolio of perhaps 150 stocks. If this is still too large a portfolio, the screens can be made tighter. As data on the financial details of firms become more accessible, these screens have also become easier to use. The key questions then become which screens to use and what priority to assign to them - i.e., which screens should be primary screens and which should be secondary screens.
There is a tremendous body of literature looking at inefficiencies in financial markets that can be of use in making these decisions. Before presenting this evidence it is important to make the following caveats:
1. To test whether a screen works, we have to compare the actual returns obtained from a portfolio using the screen to the expected returns on that portfolio. To get the expected returns on a portfolio, we need to measure the risk on that portfolio and come up with the return we should have made, given that risk. Though there are risk and return models that are used in these studies, there is (a) no consensus on what the right model for risk is and (b) significant noise in estimation within each of these models. Thus, what a study calls an "excess return" from a screen may really be the result of the use of the wrong model for risk and return.
2. Measuring actual returns is not as simple as it sounds. While most studies assume that you can buy at a price listed on a database (a closing price or a trading price) and sell later at another listed price, there are three potential pitfalls. First, it might not be possible to execute an order (buy or sell) at the listed price; this will be the case, for instance, when a strategy requires short selling and there are practical and institutional restrictions on short selling. Second, even if it is possible to execute, there might be a price impact that reduces the return; buying the asset might push up the price of the asset, and selling it may push it down, resulting in much lower returns in practice. Third, there are transactions costs in the form of brokerage costs, but more importantly, the bid-ask spread, that may also reduce the returns.
3. Finally, even if the actual returns are measured correctly and are greater than the expected returns are commensurate with the risk, the strategy itself might not make money in practice because it can be imitated by others at little cost. Thus, the excess returns that inspired the strategy may be short lived.
These three factors may explain a major contradiction in empirical analysis of investment strategies. There are literally dozens of strategies, that at least in the empirical studies that test them, seem to create excess returns for investors. There are, however, very few active investors who make excess returns, often using these same strategies. It is difficult and daunting to list out all of the empirical irregularities that investigators have found in asset returns, but we will summarize some of the key results in two groups. The first group will list out the primary inefficiencies that have been uncovered over time in financial markets in some detail; the second group will list out secondary inefficiencies that also seem to create excess returns, though the magnitude may be smaller and the results more contested, in summary.
Looking at the cross section of empirical studies of investment strategies, there are four strong "anomalies" that seem to have persisted over time. First, small companies (measured in terms of market capitalization) seem to earn higher returns, after adjusting for risk, than larger companies. Second, low price-earnings ratio stocks seem to earn excess returns relative to high price-earnings ratio stocks after adjusting for risk. Third, low price-book value stocks seem to provide a much better trade off between risk and returns than high price-book value stocks. Finally, low price-sales ratio stocks seem to be much better investments, when returns and risk are considered, than high price-sales ratio stocks.
A. The Size Effect
Studies have consistently found that smaller firms (in terms of market value of equity) earn higher returns than larger firms of equivalent risk, where risk is defined in terms of the market beta. Figure 1 summarizes returns for stocks in ten market value classes, for the period from 1927 to 1983.
The size of the small firm premium, while it has varied across time, has been generally positive, as measured in Figure 2, which summarizes small stock premiums from 1926 to 1990.
Figure 2: Small Stock Premiums from 1926 to 1990
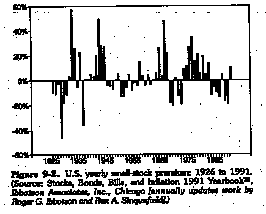
The small firm effect was strongest between 1974 and 1983. Professor Jeremy Siegel has argued in recent years that there is no small firm effect if this period is not considered. To us, though, this applies selective logic, since it throws out one set of outliers while preserving the other, which in the case of small stocks, would be the last decade (1986-96).
The small firm premium uncovered in these studies has lead to several possible explanations.
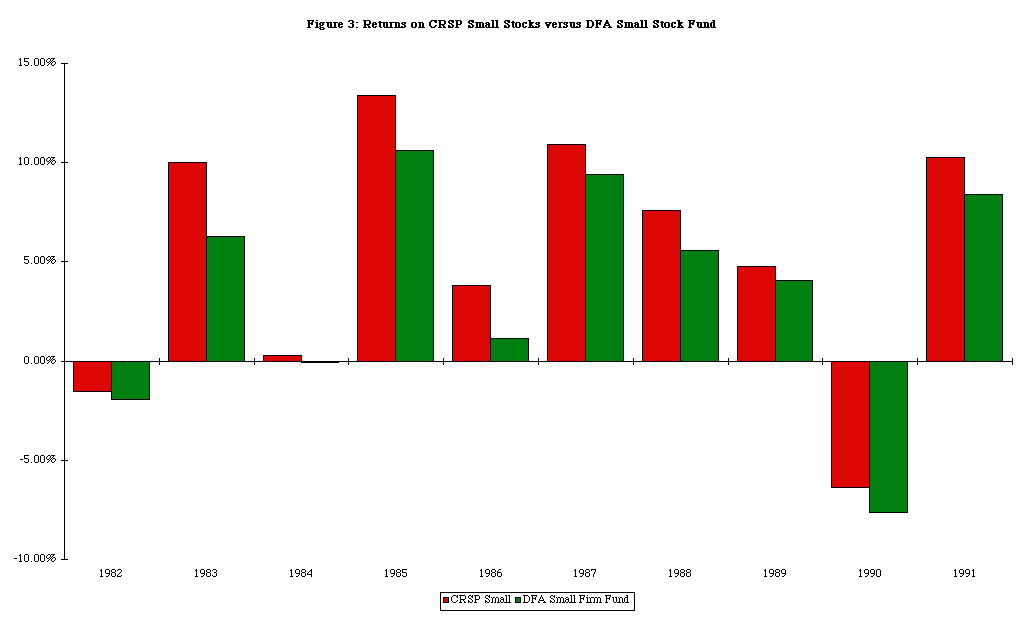
(a) The transactions costs of investing in small stocks is significantly higher than the transactions costs of investing in larger stocks, and the premiums are estimated prior to these costs. While this is generally true, the differential transactions costs are unlikely to explain the magnitude of the premium across time, and are likely to become even less critical for longer investment horizons. The difficulties of replicating the small firm premiums that are observed in the studies in real time are illustrated in Figure 3, which compares the returns on a hypothetical small firm portfolio (CRSP Small Stocks) with the actual returns on a small firm mutual fund (DFA Small Stock Fund), which passively invests in small stocks.
(b) The capital asset pricing model may not be the right model for risk, and betas may under estimate the true risk of small stocks. Thus, the small firm premium may really be a measure of the failure of beta to capture risk. The additional risk associated with small stocks may come from several sources. First, the estimation risk associated with estimates of beta for small firms is much greater than the estimation risk associated with beta estimates for larger firms. The small firm premium may be a reward for this additional estimation risk. Second, there may be additional risk in investing in small stocks because far less information is available on these stocks. In fact, studies indicate that stocks that are neglected by analysts and institutional investors earn an excess return that parallels the small firm premium.
There is evidence of a small firm premium in markets outside the United States as well. Dimson and Marsh examined stocks in the United Kingdom from 1955 to 1984 and found that the annual returns on small stocks exceeded that on large stocks by 7% annually over the period. Bergstrom, Frashure and Chisholm report a large size effect for French stocks (Small stocks made 32.3% per year between 1975 to 1989, while large stocks made 23.5% a year), and a much smaller size effect in Germany. Hamao reports a small firm premium of 5.1% for Japanese stocks between 1971 and 1988.
B. Low Price Earnings Ratio Stocks
Investors have long argued that stocks with low price earnings ratios are more likely to be undervalued and earn excess returns. For instance, Ben Graham, in his investment classic "The Intelligent Investor", uses low price earnings ratios as a screen for finding under valued stocks. Studies which have looked at the relationship between PE ratios and excess returns confirm these priors. Figure 4 summarizes annual returns by PE ratio classes for stocks from 1967 to 1988.
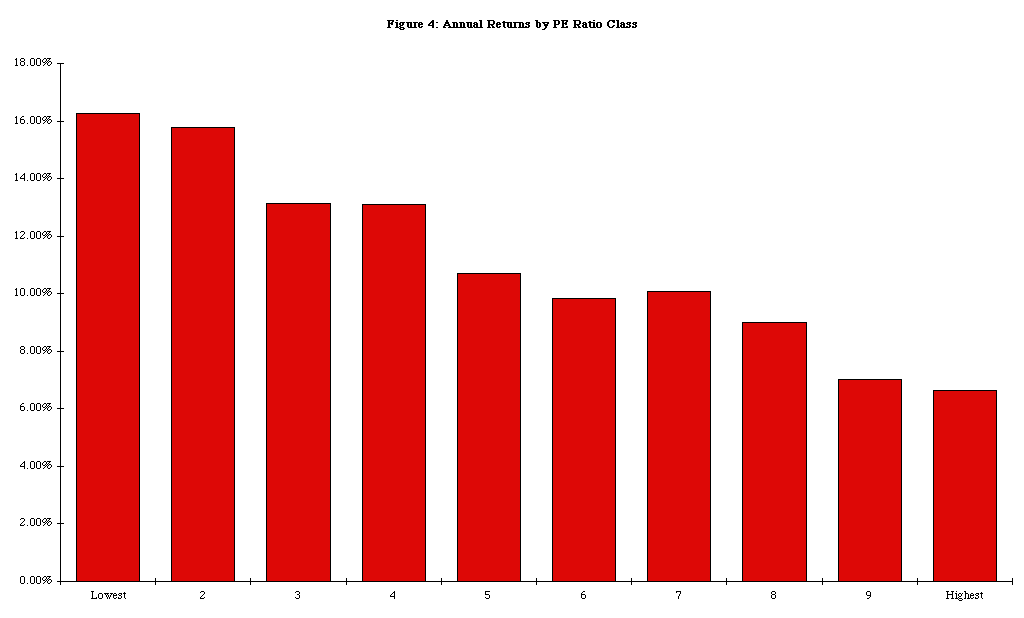
Firms in the lowest PE ratio class earned an average return of 16.26% during the period, while firms in the highest PE ratio class earned an average return of only 6.64%.
The excess returns earned by low PE ratio stocks persist in other international markets. Table 3 summarizes the results of studies looking at this phenomenon in markets outside the United States.
Table 3: Excess Returns on Low P/E Ratio Stocks by Country: 1989-1994
|
|
|
|
Australia
|
|
|
France
|
|
|
Germany
|
|
|
Hong Kong
|
|
|
Italy
|
|
|
Japan
|
|
|
Switzerland
|
|
|
U.K.
|
|
Annual premium: Premium earned over an index of equally weighted stocks in that market between January 1, 1989 and December 31, 1994. These numbers were obtained from a Merrill Lynch Survey of Propreitary Indices.
The excess returns earned by low price earnings ratio stocks are difficult to justify using a variation of the argument used for small stocks, i.e., that the risk of low PE ratios stocks is understated in the CAPM. Low PE ratio stocks generally are characterized by low growth, large size and stable businesses, all of which should work towards reducing their risk rather than increasing it. The only explanation that can be given for this phenomenon, which is consistent with an efficient market, is that low PE ratio stocks generate large dividend yields, which would have created a larger tax burden in those years where dividends were taxed at higher rates.
c. Low Price- Book Value Ratio Stocks
Another statistic that is widely used by investors in investment strategy is price book value ratios. A low price book value ratio has been considered a reliable indicator of undervaluation in firms. In studies that parallel those done on price earnings ratios, the relationship between returns and price book value ratios has been studied. The consistent finding from these studies is that there is a negative relationship between returns and price book value ratios, i.e., low price book value ratio stocks earn higher returns than high price book value ratio stocks.
Rosenberg, Reid and Lanstein (1985) find that the average returns on U.S. stocks are positively related to the ratio of a firm's book value to market value. Between 1973 and 1984, the strategy of picking stocks with high book/price ratios (low price-book values) yielded an excess return of 36 basis points a month. Fama and French (1992), in examining the cross-section of expected stock returns between 1963 and 1990, establish that the positive relationship between book-to-price ratios and average returns persists in both the univariate and multivariate tests, and is even stronger than the size effect in explaining returns. When they classified firms on the basis of book-to-price ratios into twelve portfolios, firms in the lowest book-to-price (higher P/BV) class earned an average monthly return of 0.30%, while firms in the highest book-to-price (lowest P/BV) class earned an average monthly return of 1.83% for the 1963-90 period.
Chan, Hamao and Lakonishok (1991) find that the book-to-market ratio has a strong role in explaining the cross-section of average returns on Japanese stocks. Capaul, Rowley and Sharpe (1993) extend the analysis of price-book value ratios across other international markets, and conclude that value stocks, i.e., stocks with low price-book value ratios , earned excess returns in every market that they analyzed, between 1981 and 1992. Their annualized estimates of the return differential earned by stocks with low price-book value ratios, over the market index, were as follows:
Country Added Return to low P/BV portfolio
France 3.26%
Germany 1.39%
Switzerland 1.17%
U.K 1.09%
Japan 3.43%
U.S. 1.06%
Europe 1.30%
Global 1.88%
A caveat is in order. Fama and French point out that low price-book value ratios may operate as a measure of risk, since firms with prices well below book value are more likely to be in trouble and go out of business. Investors therefore have to evaluate for themselves whether the additional returns made by such firms justifies the additional risk taken on by investing in them.
e. Low Price-Sales Ratio Stocks
Screening stocks on the basis of price-sales multiples has been incorporated by some investors into their investment strategies. In recent years, evidence has been accumulating that this strategy may yield excess returns to investors. In a direct test of the price-sales ratio, Senchack and Martin (1987) compared the performance of low price-sales ratio portfolios with low price-earnings ratio portfolios, and concluded that the low price-sales ratio portfolio outperformed the market but not the low price-earnings ratio portfolio. They also found that the low price-earnings ratio strategy earned more consistent returns than a low price-sales ratio strategy, and that a low price-sales ratio strategy was more biased towards picking smaller firms. Jacobs and Levy (1988a) tested the value of low price-sales ratios (standardized by the price-sales ratio of the industries in which the firms operated) as part of a general effort to disentangle the forces influencing equity returns. They concluded that low price-sales ratios, by themselves, yielded an excess return of 0.17% a month between 1978 and 1986, which was statistically significant. Even when other factors were thrown into the analysis, the price-sales ratios remained a significant factor in explaining excess returns (together with price-earnings ratio and size).
The significance of profit margins in explaining price-sales ratios suggests that screening on the basis of both price-sales ratios and profit margins should be more successful at identifying undervalued securities. To test this proposition, the stocks on the New York Stock Exchange were screened on the basis of price-sales ratios and profit margins to create 'undervalued' portfolios (price-sales ratios in the lowest quartile and profit margins in the highest quartile) and 'overvalued' portfolios (price-sales ratios in the highest quartile and profit margins in the lowest quartile) at the end of each year from 1981 to 1990. The returns on these portfolios in the following year are summarized in the following table:
Year Undervalued Overvalued S & P 500
Portfolio Portfolio
1982 50.34% 17.72% 40.35%
1983 31.04% 6.18% 0.68%
1984 12.33% -25.81% 15.43%
1985 53.75% 28.21% 30.97%
1986 27.54% 3.48% 24.44%
1987 -2.28% 8.63% -2.69%
1988 24.96% 16.24% 9.67%
1989 16.64% 17.00% 18.11%
1990 -30.35% -17.46% 6.18%
1991 91.20% 55.13% 31.74%
1982-91 23.76% 15.48% 17.49%
During the period, the undervalued portfolios outperformed the overvalued portfolios in six out of the ten years, earning an average of 8.28% more per year, and averaged a significantly higher return than the S&P 500.
II. Secondary Inefficiencies
In addition to these primary inefficiencies, researchers have uncovered a number of other factors that are correlated with returns. While a listing of these factors may be useful, it is worth making three points. First, some of these factors are highly correlated with the four primary factors listed above. For instance, the finding that stocks which are followed be relatively few analysts do better than those followed by lots of analysts is closely related to the size effect, since small firms tend to be followed by fewer analysts. Second, given the volume of data on stock returns that we have accumulated over time, it is not surprising that we have found a number of variables that are correlated with returns. Third, the findings on some of these factors seem to be sensitive to how the test is set up and which period is examined. Table 4 summarizes some of the secondary factors that are correlated with returns, the references for these findings and possible explanations.
E. Usage
There are clearly far more analysts who use relative valuation, especially in equity research and portfolio management, than there are those who use discounted cash flow valuation. Part of the reason for this is the ease with which relative valuation can be used to find under or over valued assets in large universes. Another reason for the attachment that equity research analysts have to multiples can be traced to the fact that they are asked to find the most under valued securities in the sectors that they follow, not make fundamental judgments about whether their sector itself is over or under valued. Similarly, investors who invest with equity money managers expect them to invest in the stocks that are most under valued in a market, and not to pass judgment on whether the market itself is under or over valued. Finally, there are some analysts who think that using multiples relieves them of the responsibility of making assumptions about variables such as net capital expenditures and growth in future years.
F. Limitations of Relative Valuation
The strengths of relative valuation are also its weaknesses. While relative valuation allows analysts and money managers to find under valued assets with ease in any market, it may also blind those who use it to significant misvaluation in a sector or the entire market. To provide a illustration, it would be possible, using multiples and comparables, to find "under valued stocks" in a sector that is itself over valued by 40 or 50%. Even if the relative valuation is done with care, all this "under valuation" implies is that if there is a price correction in the sector, the undervalued stock will lose less in value than the comparable firms. Since the better choice for the investor would have to been to avoid the sector all together, relative valuation can lead to returns that are lower than would have been obtained by using intrinsic valuation models. Even when relative valuation is done a market wide basis, there is a risk that the entire market is price too high, relative to its fundamentals, and an intrinsic valuation model may have exposed this under valuation and allowed the investor to steer clear of the market.
III. Technical Analysis Models
Technical analysis refer to the use of price charts, trading volume and other indicators based upon market activity to find under and over valued assets. While technical analysis is widely used by investors, its value has been challenged not only be academics who have looked at the performance of some technical indicators but also by practitioners who use multiples or fundamentals as, as voodoo investing with no basis in either theory or evidence. In this section, we will take a much more sympathetic view of technical analysis that looks at many of its weaknesses but also considers some of its strengths that may account for the following it has on investors.
A. Basis for Approach
To understand the basis for technical analysis, we went back to one of its early proponents. Levy argued for technical analysis, noted that market value was determined by supply and demand, and that each was governed by both rational and irrational factors. The irrational factors, he further argued, caused stock prices to move in trends which persist over appreciable lengths of time; the purpose of technical indicators is to detect shifts in these trends. Thus, all technical indicators are built on the assumption that markets are irrational and that technical indicators give early signals of these irrationalities can be taken advantage of.
Historians who have examined the behavior of financial markets over time have challenged the assumption of rationality that underlies much of efficient market theory. They point out to the frequency with speculative bubbles have formed in financial markers, as investors buy into fads or get-rich-quick schemes, and the crashes with these bubbles have ended, and suggest that there is nothing to prevent the recurrence of this phenomenon in today's financial markets. There is some evidence, in the literature, of irrationality on the part of market players.
While most experimental studies suggest that traders are rational, there are some examples of irrational behavior in some of these studies. One such study was done at the University of Arizona. In an experimental study, traders were told that a payout would be declared after each trading day, determined randomly from four possibilities - zero, eight, 28 or 60 cents. The average payout was 24 cents. Thus the share's expected value on the first trading day of a fifteen day experiment was $3.60 (24*15), the second day was $3.36 .... The traders were allowed to trade each day. The results of 60 such experiments is summarized in figure 5.
Figure 5: Experimental study of Price Behavior
There is clear evidence here of a 'speculative bubble' forming during periods 3 to 5, where prices exceed expected values by a significant amount. The bubble ultimately bursts, and prices approach expected value by the end of the period. If this is feasible in a simple market, where every investor obtains the same information, it is clearly feasible in complex financial markets, where there is much more differential information and much greater uncertainty about expected value.
B. Types of Technical Indicators
Since technical indicators are built on the premise of investor irrationality, it makes sense to classify these indicators based upon the type of irrationality that they are premised upon.
I. Investors Overreact To Information Announcements
Research in experimental psychology suggests that people tend to overreact to unexpected and dramatic news events. In revising their beliefs, individuals tend to overweight recent information and underweight prior data. There are several technical indicators that are built upon this premise. First, is the odd-lot rule which looks at the proportion of odd-lot trades (i.e., trades of less than 100 shares) to total trades. Since odd lots are usually traded by small investor, this rule gives us an indication of what small investors think about the stock. It then assumes that the small investors are wrong and pursues strategies opposite to their thinking. A second technical indicator that builds on the assumption that investors over react is the cash position of mutual funds. This statistic, which is widely reported, measures the cash held by mutual funds as a percentage of total funds. A low number here would indicate that fund managers are bullish about stocks and a high number would indicate bearishness. Historically, the argument goes, mutual fund cash positions have been greatest at the bottom of a bear market and lowest at the peak of a bull market. Hence, investing against this statistic may be profitable. A third technical indicator measures bullishness among investment advisors. Here again, the argument is that advisors tend to overreact; consequently, it makes sense to buy when investment advisors are most bearish about a stock or a market and to sell when they are most bullish about the same.
II. Investor Mood Changes Lead to Shifts In Demand And Supply
While the notion that prices are determined by demand and supply is one that all investors would agree upon, there are some technical analysts who argue that shifts in demand and supply can be detected by price and volume patterns. One indicator is the breadth of the market, which is a measure of the number of stocks in the market which have advanced relative to those that have declined. Thus, a market which goes up with little breadth, is considered to be a market on verge of a shift downwards in demand (and thus in price). For individual stocks, there are scores of price patterns that are viewed as precursors of shifts in demand and hence prices - for instance, the price breaking through a resistance line (which is viewed as a bullish sign) or through a support line (which is viewed as a bearish sign) or the price exceeding the moving average of prices over some prior period (which is viewed as bullish sign) or dropping below the moving average.
Iii. Markets Learn Slowly: The Momentum Investors
The argument here is that markets learn slowly. Thus, investors who are a little quicker than the market in assimilating and understanding information will earn excess returns. In addition, if markets learn slowly, there will be price drifts (i.e., prices will move up or down over extended periods) and technical analysis can detect these drifts and take advantage of them.
There is evidence, albeit mild, that prices do drift after significant news announcements. For instance, following up on price changes after large earnings surprises provides the evidence in Figure 6.
Figure 6: Price Reactions to Earnings Announcements
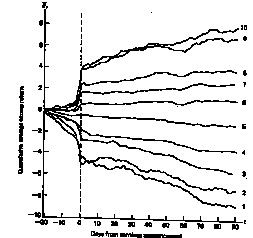
Portfolio 10 includes those stocks with the biggest positve earnings surprises, and portfolio 1 those stocks with the most negative earnings surprises. Figure 6 graphs out the price behavior of stocks in each portfolio in the 60 days following the announcement Note the price drift, especially after the most extreme earnings announcements.
One of the indicators most widely used by momentum investors is the relative strength of a stock. The relative strength of a stock is the ratio of its current price to its average over a longer period (e.g. six months). The rule suggests buying stocks which have the highest relative strength (which will also be the stocks that have gone up the most in that period) and selling stocks which have gone down the most over the same period.
IV. Markets Are Controlled By External Forces: The Mystics
There are some technical indicators that are based upon the view that markets are governed by factors are "external"; without prejudice, one could call this the "Karma Approach" to investing. For instance, Elliot's theory is that the market moves in waves of various sizes, from those encompassing only individual trades to those lasting centuries, perhaps longer. As one proponent put it, ".. by classifying these waves and counting the various classifications it is possible to determine the relative positions of the market at all times". There can be no bull of bear markets of one, seven or nine waves, for example.
In the Dow Theory, the market is always considered as having three movements, all going at the same time. The first is the narrow movement (daily fluctuations) from day to day. The second is the short swing (secondary movements) running from two weeks to a month and the third is the main movement (primary trends) covering at least four years in its duration.
V. Following The Smart Investors: The Followers
The final set of technical indicators are built on the assumption that some investors are smarter than others and that indicators that can capture what the "smart" investors are doing will allow us to make excess returns. A good example of such an indicator would the specialists’ short sales ratio, which looks at short selling by specialists (who presumably know more about the stock than other investors) as a proportion of total trading volume; high short selling by specialists would be viewed as a "bearish" indicator. Another indicator that is used looks at insider buying or selling on a stock; high insider buying (selling) would be viewed as a bullish (bearish) indicator. There is some empirical evidence that buying stocks where insider buying is strong and selling stocks where insider selling is strong may yield excess returns, and that these returns increase with the "importance" of the insider; a CEO buying stock in his or her own company is a more positive indicator than a subordinate doing the same. This evidence has to be tempered by counter-evidence that suggests that these excess returns are sensitive to when the investment is made; investments made on the date of the insider report to the SEC make excess returns, but these returns dissipate if the investments are made when the actual SEC report is made public.
It is worth noting that this approach often is in direct contradiction to the first approach described in this section, which assumes that investors over react. Thus, the same indicator that may lead some investors (the contrarians) to sell may lead other investors (the followers of smart investors) to buy.
C. Usage and Empirical Evidence
There has long been a deep divide between what non-technicians think about technical analysis and its adherents. While the former are convinced that charts and technical indicators are useless in finding undervalued assets, technical analysts are equally adamant in claiming that they are wrong. Until recently, each side was able to cite studies that showed its view of the world was right. Given the strong biases within each group, these findings were not surprising. In recent years, however, many researchers have uncovered surprisingly strong evidence that there are predictable patterns in the prices of assets. These findings should come as small consolation for technical analysts, however, since many of the patterns are long term and are unlikely to be captured by most technical indicators.
1. Long Term Price Reversals
There is substantial negative correlation in longer term return intervals, suggesting that markets reverse themselves over very long periods. Since such behavior, if true, would be a serious challenge to market efficiency, the phenomenon has been examined in extensive detail. Studies that break down stocks on the basis of market value have found that the serial correlation is more negative in five-year returns than in one-year returns, and is much more negative for smaller stocks rather than larger stocks. Figure 7 summarizes one-year and five-years serial correlation by size class for stocks on the New York Stock Exchange.
Figure 7: One-year and Five-year Serial Correlations - By Size Class
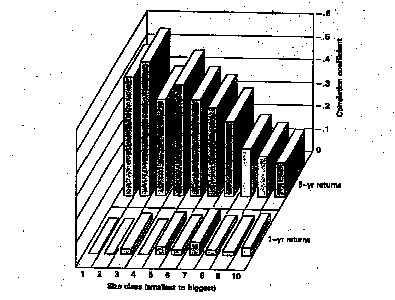
This phenomenon has also been examined in other markets, and the findings have been similar. There is evidence that returns reverse themselves over long time period.
Since there is evidence that prices reverse themselves in the long term for entire markets, it might be worth examining whether such price reversals occur on classes of stock within a market. For instance, are stocks which have gone up the most over the last period more likely to go down over the next period and vice versa? To isolate the effect of such price reversals on the extreme portfolios, DeBondt and Thaler constructed a winner portfolio of 35 stocks, which had gone up the most over the prior year, and a loser portfolio of 35 stocks, which had gone down the most over the prior year, each year from 1933 to 1978, and examined returns on these portfolios for the sixty months following the creation of the portfolio. Figure 8 summarizes the excess returns for winner and loser portfolios.
Figure 8: Excess Returns for Winner and Loser Portfolios
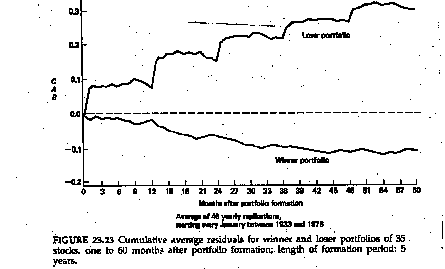
This analysis suggests that loser portfolio clearly outperform winner portfolios in the sixty months following creation. This evidence is consistent with market overreaction and correction in long return intervals.
There are many, academics as well as practitioners, who suggest that these findings may be interesting but that they overstate potential returns on 'loser' portfolios. For instance, there is evidence that loser portfolios are more likely to contain low priced stocks (selling for less than $5), which generate higher transactions costs and are also more likely to offer heavily skewed returns, i.e., the excess returns come from a few stocks making phenomenal returns rather than from consistent performance. One study of the winner and loser portfolios attributes the bulk of the excess returns of loser portfolios to low-priced stocks and also finds that the results are sensitive to when the portfolios are created. Loser portfolios created every December earn significantly higher returns than portfolios created every June.
2. Price Momentum
In direct contradiction of the previous finding is another pattern that was uncovered by Jegadeesh and Titman(1993). They tested a trading strategy of buying past winners and losers, based upon price performance over the previous six months, and holding for the next six months, and realized an excess return of 12%. Furthermore, they found that these excess returns persisted even after correcting for other know anomalies such as market capitalization. They did find, however, that this approach lost money in January, but made excess returns in every other month of the year. They attribute much of the excess returns to a delayed reaction to information, since the winner (loser) stocks make much of their positive (negative) excess returns around earnings announcements. This should offer solace to technical analysts who use relative strength (both price and earnings), which is a measure of past price and earnings performance.
D. Limitations of Technical Analysis
The empirical evidence that has emerged in recent years on patterns that exist in stock and bond prices has made technical analysis more respectable. In addition, a combination of better data (intraday price movements), more sophisticated approaches to analyzing price and volume data (for instance, the emergence of chaos theory and neural networks), and more powerful computers has allowed technical analysis to move beyond just charts and broad volume indicators. Each of these advances, however, has come with costs. The proliferation of data has opened up the possibility of "data mining", i.e., a researcher looking at a large enough data set and enough technical indicators and models will always find a few that work over a specific period. It is unlikely, however, that they will provide excess returns in the future. This problem worsens as models become more complex and mathematical (and less intuitive), which indicates that some of the findings on stock price predictability emerging from the "new’ technicians (chaos theory, neural networks etc.) have to be used with caution.
IV. Private Information
Private information refers to information about an asset that is available on to one or a few investors interested in it and not to others. It remains the surest way of making excess returns in a market, but it may also have a fatal flaw. In some markets, its use is specifically prohibited, as is the case with insider trading laws in the stock markets in the United States.
A. What is private information?
Defining private information is actually more difficult than it would seem at the outset. While it refers to information about an investment that is available only to a subset of the investors of the asset and not to all, its value is diluted rapidly as the size of the subset increases. Furthermore, the information itself may take several forms. It may be about a specific event relating to a firm, such as an earnings announcement or a takeover bid by a firm, that has not been made public yet but will happen in the near future. It may be a more general aggregation of private information about the prospects for a firm, such as an increase in the availability of new projects or improvements in profitability of key segments that might not be visible to other investors, that leads to an increase in the assessed value for the asset. Insider trading laws generally prevent investors from trading on the former but not on the latter.
Private information can also be categorized based upon the precision of the information. It can be perfect, in which case there is no likelihood that the information is false and the effects on the price of the asset are unambiguous (at least in terms of direction). Thus, a true insider (such as a manager in the firm or a director) may be able to get precise information about a takeover bid that will be made tomorrow. It can be noisy, in which case there is a chance that either the information is false or misleading. This may be the case when an outsider learns of this information through second hand sources or as is often the case in markets, through rumors. It may also be that an investor has private information about a firm, but is uncertain about the implications for value. While profits are certain in the first scenario (where information is perfect), they are uncertain in the latter when it is noisy or its implications are uncertain; on average, however, there should be positive returns associated with getting even imprecise private information.
B. Using Private Information
The way in which investors use private information to pick assets is determined by two factors - the precision of the information and the legality of using the information. At one end of the continuum, an investor in possession of perfect inside information with no constraints on legality of trading can take full advantage of the information by trading in the asset or its derivatives directly, and buying and selling as much he or she can of that asset or derivative. There will be no need to hedge risk or hold a diversified position, since the payoff is guaranteed, though the exact magnitude of the payoff may be unclear. At the other end of the continuum, an investor who hears a rumor about an asset and is unclear about both the authenticity of the information and its effect on the asset’s price may decide to take either a very limited position in the asset, take a larger position and hedge the risk partially or take positions in more than one asset (i.e., diversify). When trading on the asset is illegal, investors cannot take positions in either the traded asset or its derivatives without running afoul of the law. Of course, this technicality has not deterred investors from doing so anyway, using intermediaries and third parties to disguise their actions.
C. Usage and Empirical Evidence
Do investors use "private" information to pick under and over valued assets? Do they make excess returns when they do? We do not need extended studies to know that the answer is yes to both. In fact, since it is illegal to do the former, no study that uses public databases of insider trading such as the SEC official summary of insider trading, is going to be able to answer these questions. The indirect evidence is overwhelming, though, that insiders make significant profits in most markets. On the first question, the price run-up that we often observe before significant information announcements (e.g., earnings and merger announcements) suggests either an incredibly perceptive market or information leakage somewhere along the way. The surge in trading volume, often in the derivatives markets, before significant news announcements is another piece of evidence that investors do have access to private information and use it. On the second question, the evidence is partly anecdotal and it comes from looking at the profits of insiders who get caught using private information. The other evidence comes from looking at the subset of insider trading that is legal and hence summarizes in the SEC databases.
The SEC defines an insider to be a officer or director of the firm or a major stockholder (holding more than 5% of the outstanding stock in the firm). Insiders are barred from trading in advance of specific information on the company and are required to file with the SEC when they buy or sell stock in the company. If it is assumed, as seems reasonable, that insiders have better information about the company, and consequently better estimates of value, than other investors, the decisions by insiders to buy and sell stock should affect stock prices. Figure 9, derived from an early study of insider trading by Jaffe, examines excess returns on two groups of stock, classified on the basis of insider trades. The "buy group" includes stocks where buys exceeded sells by the biggest margin, and the "sell group" includes stocks where sells exceed buys by the biggest margin.
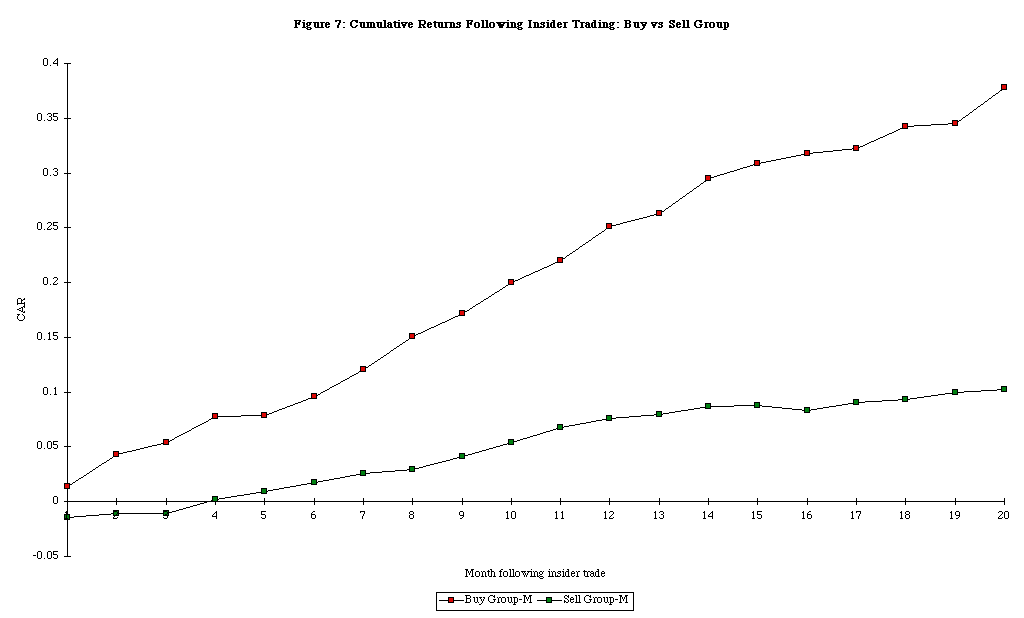
D. Limitations of Private Information
There is a case to be made that the difference between a successful investor and an unsuccessful one is the difference in the quality of information possessed by each. There are three requirements, however, that have to be met to invest successfully with private information:
(1) The investor has to have and maintain access to high quality private information.
(2) The investor has to be able to trade on that information without revealing it instantaneously.
(3) The use of the information has to be legal.
There are problems with meeting each of these requirements. First, it is difficult to have access to good private information without being an insider, either as a top manager in the firm or firms affected by the information or as an advisor (investment banker or accountant) to these firms. Since these are exactly the conditions under which trading is illegal, at least in the United States, the third requirement of legality will not be met. As an outsider to the firm, access to this information is either second-hand or through rumors, which effectively reduces the quality of the information and makes it more hazardous to create effective strategies. Second, even if an investor has access to good private information, the process of trading on that information may itself reveal the nature of the information (whether it is good or bad news) to the rest of the market and reduce or eliminate the excess returns that can be earned. This is of particular concern since strategies that try to take advantage of private information tend to be short term and create substantial transactions costs. Third, an investor who has acquired good private information and traded on it effectively may find himself or herself the target of a problem by the SEC, since it is the existence of large profits that evokes suspicion that insider information may have been used. While there might ultimately be no legal sanction, it is a costly and risky process given the vagueness of the insider trading law on who exactly is an insider and what comprises insider trading.
In summary, the profits from using private information make it seem like an attractive option to many investors. However, strategies that use private information may actually be much riskier in practice, from both an economic and legal standpoint, than they seem from the outside.
The strategies described so far are active strategies which attempt to find undervalued and overvalued securities, using valuation models, multiples, charts or private information. While these strategies vary immensely in their philosophical bases and in their execution, they do share some common characteristics. They are all costly, in terms of the time and the resources that are needed to find the misvalued securities and transactions costs, though the costs may vary across strategies. They are also likely to result in portfolios that over weight some sectors, relative to their value, and under weight others., leading to a loss in diversification benefits. Investors are willing to live with these costs as long as the benefits that they provide exceed the costs. In this section, we will examine whether active asset selection, at least on average, yields a benefit that exceeds the cost, and we will consider the passive alternative (indexing) which allocates the portfolio across assets in each asset class based upon market value.
The Case Against Active Asset Selection
The best case against active asset allocation is made, ironically, by active portfolio managers. Professional money managers operate as the experts in the field of investments. They are supposed to be better informed, smarter, have lower transactions costs and be better investors overall than smaller investors. The earliest study of mutual funds by Jensen suggested that this supposition might not hold in practice. His findings, summarized in Figure 10, as excess returns on mutual funds, were that the average portfolio manager actually underperformed the market between 1955 and 1964.
These results have been replicated with mild variations in the conclusions. In the studies that are most favorable for professional money managers, they break even against the market after adjusting for transactions costs, and in those that are least favorable, they underperform the market even before adjusting for transactions costs. To those who would argue that these results are because of "risk" adjustments that are unfair to money managers, the underperformance of active money managers can be illustrated by looking at their performance relative to the S&P 500. Figure 11 summarizes the percentage of active equity money managers who were beaten by the S&P 500 index between 1986 and 1995.
The evidence is no more promising when we look at Figure 12, which summarizes the performance of active bond fund managers relative to a bond index.
The average bond fund underperformed the Lehman index by approximately 1.5%.
The results, when categorized on a number of different basis, do not offer much solace. For instance, Figure 13 shows excess returns from 1983 to 1990, and the percentage of money managers beating the market, categorized by investment style.
Money managers in every investment style underperform the market index.
Figure 14, from the same study, looks at the payoff to active portfolio management by looking at the added value from trading actively during the course of the year and finds that returns drop from 0.5% to 1.5% a year as a consequence.
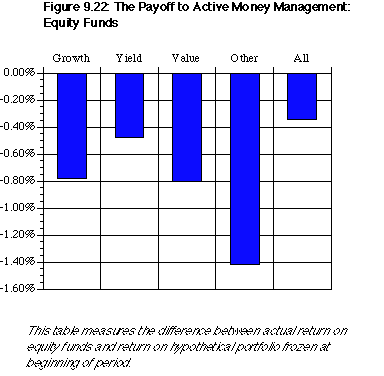
Finally, the study, like others before it, found no evidence of continuity in performance. It classified money managers into quartiles and examined the probabilities of movement from one quartile to another each year from 1983 to 1990. The results are summarized in Table 5.
Table 5: Probabilities of Transition from One Quartile to Another
|
|
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
This table indicates that a money manager who was ranked in the first quartile in a period had a 26% chance of being ranked in the first quartile in the next period and a 27% chance of being ranked in the bottom quartile. There is some evidence of reversal in the portfolio managers in the lowest quartile, though some of that may be a reflection of the higher risk portfolios that they put together.
The sole hopeful note in the studies is that there are a few areas where active money managers seem to have outperformed the indices. One area is in international asset allocation, where active money managers have beaten the "passive" allocation model recently, though almost all of the outperformance in recent years can be attributed to managers underweighting Japanese stocks in their portfolios. The other is active funds in "emerging" and "information poor" markets, which do better than passive funds in these markets. This may be attributable to the better information and superior execution skills that these funds may have over other investors in these markets.
In summary, active portfolio managers, on average, underperform market indices. The underperformance is broad based and cannot be attributed to "risk" adjustments or to a few poor active money managers. Given that investors have to pay extra fees for active money management, it is not surprising that many of them turn to indexing.
Indexing
The case against active investing is strong enough for some investors to consider an alternative, which is to allocate the portfolio across assets in the asset class based upon the market value of each asset. This approach is called indexing, and an index fund attempts to replicate a market index for the asset class; with stocks, index funds often try to replicate the S&P 500, with bonds, the Lehman bond index, and with international stocks, the Morgan Stanley Capital Index.
A. Mechanics of Indexing
The mechanics of creating an index fund are simple. The first step is to identify the index that the fund plans to replicate. While diversification would argue for replication of the widest possible index, transactions costs and the dependability of the indices in use may result in narrower indices being chosen. Thus, in the United States, the most widely replicated index is the S&P 500 even though the NYSE composite or the Wilshire 5000 may be broader indices. The second step is to estimate the market values of the assets in the index, and calculate the market value weights of the assets. The final step is to create a portfolio of the assets in the index, with the same market value weights. This process, which allows for perfect replication, becomes costly when the index contains thousands of assets. In such a case, the index fund may reduce its costs by using sampling to create a portfolio with the same characteristics as the index (sector weights, market capitalization etc.). This sampling strategy does come with a cost - the index fund will no longer perfectly replicate the index, but will follow the index with noise.
Index funds are, for the most part, self-correcting, since assets in the fund and assets in the index essentially move together. It does need to be adjusted as new assets enter the index, and old assets leave the index.
B. Advantages of Indexing
Index funds have two advantages of traditional actively managed funds. First, there are no information costs or analyst expenses associated with running these funds, and there are little transactions costs associated with trading. Most index funds have turnover ratios of less than 5%, indicating that the total dollar volume of trading was less than 5% of the market values of the funds. This results in transactions costs at these funds of 0.20%-0.50%, which is less than one third the costs at most actively managed funds. Second, the index funds’ reticence to trade also reduces the tax liabilities that they create for investors. In a typical actively managed fund, the high turnover ratios create capital gains and tax liabilities even for those investors who buy and hold these funds. The following figure, replicated from John Bogle’s book on mutual funds, measures the difference between pre-tax and after-tax returns at several funds.
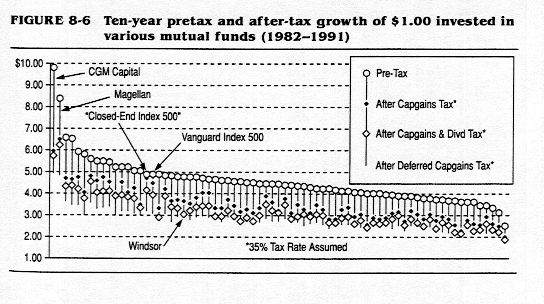
C. Limitations of Indexing
The primary limitation of index funds is that they cannot deliver more than they promise, which is to keep up with the index. To the extent that an investor wants to beat the market, this may not be satisfactory. It can also be argued that the tendency of index funds to replicate just a few well know indices (such as the S&P 500) can result in the stocks in these indices becoming over valued, especially as index funds become more popular. Furthermore, the most popular indices may not be the most diversified ones, either. This is not a problem with index funds per se, but with how most of them are constructed.
Conclusions
Investment strategies that claim to find misvalued assets abound, and can be categorized into four groups - strategies that use discounted cash flow models to value assets, relative valuation strategies that compare the pricing of individual assets to the pricing of assets that are "comparable" to them, technical analysis strategies that use price and volume indicators to predict shifts in market sentiment and strategies that attempt to use private information to find assets that are under or over valued. Many investors subscribe to more than one of these groups of strategies, but very few investors seem to succeed in using them to earn returns in excess of what they would have earned adopting a passive strategy of buying and holding a diversified portfolio of the assets. This gap between the performance that is promised by those who develop these strategies and the performance that is delivered by those who use these strategies suggests that there are significant costs and problems in execution - higher transactions costs, price impact while trading and imitation by other investors. The promise of "beating the market" is powerful enough, however, to induce investors to keep trying to come up with "new and improved" strategies. Far from bemoaning this fact, we should be celebrating it, since it is precisely this search for value that makes market price reflect information and value in the first place.