The cost of trading clearly imposes a drag on the performance of portfolio managers. As we debate the extent of these costs, we need to get a measure of what the costs are, how they vary across investment strategies and how investors can minimize these costs. In the previous chapter, Robert Arnott discussed some of the difficulties associated with the measurement of trading costs, and noted the debate between those who think trading costs are too high, taking an expansive view of what comprises these costs, and those who argue that it is negligible from the perspective of the entire market.
In this chapter, we will take a middle road, where we will look at the ingredients that go into trading costs, and examine the kinds of strategies where trading costs are likely to be high and those where they will generally be low.
While we debate what constitutes trading costs and how to measure them, there is a fairly simple way in which we can estimate, at the minimum, how much trading costs affect the returns of the average portfolio manager. Active money managers trade because they believe that there is profit in trading, and the return to any active money manager has three ingredients to it:
Return on active money manager = Expected ReturnRisk + Return from active trading - Trading costs
Looking across all active money managers, the average expected return has to be equal to the return on the market index. Thus, subtracting the average return made by active money managers from the return on the index should give us a measure of the payoff to active money management:
Average ReturnActive Money Managers - Return on Index = Return from Active Trading - Trading Costs
In chapter 8, we noted that the average active money manager has underperformed the index in the last decade by about 1%. If we take the view that active trading adds no excess return, on average, the trading costs, at the minimum, should be 1% of the portfolio on an annual basis. If we take the view that active trading does add to the returns, the trading costs will be greater than 1% of the portfolio on an annual basis.
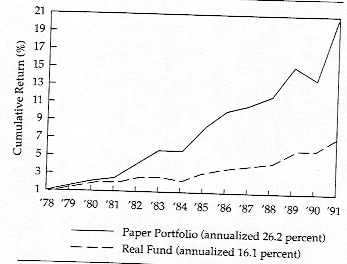
There are also fairly specific examples of real portfolios that have been constructed to replicate hypothetical portfolios, where the magnitude of the trading costs are illustrated starkly. Consider, for instance, the difference in returns between 1979 and 1991 between the fund that Value Line has run and the paper portfolio that Value Line has used to compute the returns that its stock picks would have had.
Figure 12.1: Value Line Real and Paper Portfolios

The paper portfolio had an annual return of 26.2%, whereas the Value Line fund had a return of 16.1%. While part of the difference can be attributed to Value Line waiting until its subscribers had a chance to trade, a significant portion of the difference can be explained by the costs of trading.
Looking at the evidence, there are a couple of conclusions that we would draw. The first is that money managers either under estimate the trading costs, over estimate the returns to active trading or both. The second is that trading costs are a critical ingredient to any investment strategy, and can make the difference between a successful portfolio and an unsuccessful one.
There are some investors who undoubtedly operate under the misconception that the only cost of trading is the brokerage commission that they pay when they buy or sell assets. While this might be the only cost that they pay explicitly, there are other costs that they incur in the course of trading that generally dwarf the commission cost. When trading any asset, they are three other ingredients that go into the trading costs. The first is the spread between the price at which you can buy an asset (the dealer’s ask price) and the price at which you can sell the same asset at the same point in time (the dealer’s bid price). The second is the price impact that an investor can create by trading on an asset, pushing the price up when buying the asset and pushing it down while selling. The third cost, which was first proposed by Jack Treynor in his article on transactions costs, is the opportunity cost associated with waiting to trade. While being a patient trader may reduce the first two components of trading cost, the waiting can cost profits both on trades that are made and in terms of trades that would have been profitable if made instantaneously but which became unprofitable as a result of the waiting. It is the sum of these costs, in conjunction with the commission costs, that makes up the trading cost on an investment strategy.
There is a difference between that a buyer will pay and the seller will receive, at the same point in time for the same asset, in almost every traded asset market. The bid-ask spread refers to this difference. In the section that follows, we will examine why this difference exists, how large it is as a cost, the determinants of its magnitude and its effects on returns in different investment strategies.
Why is there a bid-ask spread?
In most markets, there is a dealer or market maker who sets the bid-ask spread, and there are three types of costs that the dealer faces that the spread is designed to cover. The first is the risk cost of holding inventory; the second is the cost of processing orders and the final cost is the cost of trading with more informed investors. The spread has to be large enough to cover these costs and yield a reasonable profit to the market maker on his or her investment in the profession.
1. The Inventory Rationale
Amihud and Mendelson present a simple model of a market maker who has to quote bid prices and ask prices, at which he is obligated to execute buy and sell orders from investors. These investors, themselves, could be trading because of information they have received (informed traders), for liquidity (liquidity traders or based upon their belief that an asset is under or over valued (value traders). In such a market, setting too high a bid price will result in an accumulation of inventory to the market maker, whereas setting too low of an ask price will result in an increase in the market maker’s short position.
Amihud and Mendelson argue that market makers operate with inventory constraints, some of which are externally imposed (by the exchanges or regulatory agencies) and some of which are internally imposed ( due to financial and risk reasons). As the market maker’s inventory position deviates from his or her optimal position, the prices will be different from the preferred prices; if the inventory is too high, the prices will be lower than the preferred prices; if the inventory is too low, the prices will be higher than the preferred prices.
2. The Processing Cost Argument
Since market makers incur a processing cost with the paperwork and fees associated with orders, the bid-ask spread has to cover, at the minimum, these costs. While these costs are likely to be very small for large orders of stocks traded on the exchanges, they become larger for small orders of stocks, that might be traded only through a dealership market. Furthermore, since a large proportion of this cost is fixed, these costs as a percentage of the price will generally be higher for low-priced stocks than for high-priced stocks.
3. The Adverse Selection Problem
The adverse selection problem arises from the different motives investors have for trading on an asset - liquidity, information and views on valuation. Since investors do not announce their reasons for trading at the time of the trade, the market maker always runs the risk of trading against more informed investors. Since the expected profits from such trading are negative, the market maker has to charge an average spread that is large enough to compensate for such losses. This theory would suggest that spreads will increase with the proportion of informed traders in an asset market, the "differential" information possessed, on average, by these traders and uncertainty about future information on the asset.
The Magnitude of the Bid-Ask Spread
The New York Stock Exchange reported that the average bid-ask spread across all NYSE stocks in 1996 was $0.23, which seems trivial especially when one considers the fact that the average price of a NYSE stock is between $ 40 and $ 50. This average, however, obscures the large differences in the cost as a percentage of the price across stocks, based upon capitalization, stock price level and trading volume. A study by Thomas Loeb in 1983, for instance, reported the spread as a percentage of the stock price for companies as a function of their marker capitalization for small orders. These results are summarized in Table 12.1.
Table 12.1: Bid Ask Spread as Function of Market Capitalization
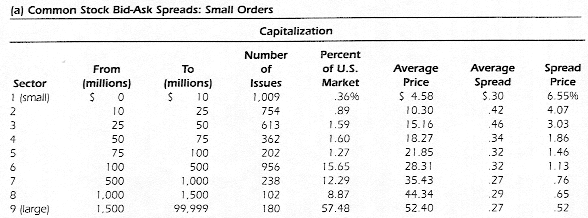
Note that the spread is as high as 6.55% of the price, for small capitalization stocks, to 0.52% of the price for large capitalization companies. Another study by Huang and Stoll found that the stocks in the top 20% in terms of trading volume had an average spread of only 0.62% while the stocks in the bottom 20% had a spread of 2.06%. There are also large differences in bid-ask spreads across different exchanges in the United States. Looking at only NASDAQ stocks, Kothare and Laux found that the average was almost 6% of the price in 1992, and much higher for low-prices stocks on the exchange. Some of the difference can be attributed to the fact that NASDAQ stocks are generally much smaller and riskier than stocks listed on the NYSE or AMEX.
While these studies looked at traded U.S. equities, there are bid-ask spreads in other markets as well. While no single comprehensive study of all these spreads exists, the following conclusions seem warranted:
The Determinants of the Bid-Ask Spread
A number of studies have looked at the variables that determine (or, at the very least, correlate with) the bid-ask spread. Studies by Tinic and West (1972), Stoll (1978) and Jegadeesh and Subrahmanyam (1993) find that spreads as a percentage of the price are correlated negatively with the price level, volume and the number of market makers, and positively with volatility. Each of these findings is consistent with the theory on the bid-ask spread. The negative correlation with price level can be explained by the higher processing cost as a percentage of the price. Higher volume reduces the need for market makers to maintain inventory and also allows them to turn over their inventory rapidly, resulting in lower inventory costs. The higher volatility leads to higher bid-ask spreads partly because the adverse selection problem is greater for more volatile stocks; there will generally be more informed traders, a greater "information differential" and greater uncertainty about future information on these stocks. It is also worth noting that variables such as price level, volatility and trading volume are not only correlated with each other, but are also correlated with other variables such as firm size.
The study quoted in the previous section, by Kothare and Laux, that looked at average spreads on the NASDAQ also looked at differences in bid-ask spreads across stocks on the NASDAQ. In addition to noting similar correlations between the bid-ask spreads, price level and trading volume, they uncovered an interesting new variable. They found that stocks where institutional activity increased significantly had the biggest increase in bid-ask spreads. While some of this can be attributed to the concurrent increase in volatility in these stocks, it might also reflect the perception on the part of market makers that institutional investors tend to be informed investors with more or better information.
Role in Investment Strategies
Looking at the evidence, it is clear that bid-ask spreads will affect the returns from investment strategies, but that the effect will vary, depending upon the strategy. While a strategy of buying under valued companies the S&P 500 and holding for the long term should not be affected very much by the bid-ask spread, a strategy of buying small over-the-counter stocks or emerging market stocks on information, and trading frequently, might lose a substantial portion of its allure, when bid-ask spreads are factored into the returns.
To show the effect of the bid-ask spread on returns, consider the strategy of buying "losers". DeBondt and Thaler(1985) present evidence that a strategy of buying the stocks which have the most negative returns over the previous year and holding for a five-year period earns significant excess returns. A follow-up study, however, noted that many of these "losers" were low-priced stocks, and that putting in a constraint that the prices be greater than $10 on this strategy resulted in a significant drop in the excess returns. Since bid-ask spreads tend to be largest for low-priced stocks, it is an open question as to whether an investment strategy of buying losers will yield excess returns in practice. In fact, similar concerns should exist about any strategy that recommends investing in low-priced, inactive and small-cap stocks, or in asset classes which have high volatility and low liquidity.
Most investors assume that trading costs become smaller as portfolios become larger. While this is true for brokerage commissions, it is not always the case for the other components of trading costs. There is one component where larger investors bear a more substantial cost than do smaller investors and that is in the impact that trading has on prices. If the basic idea behind successful investing is to buy low and sell high, pushing the price up as you buy and then down as you sell reduces the profits from investing.
Why is there a price impact?
There are two reasons for the price impact, when investors trade. The first is that markets are not completely liquid. A large trade can create an imbalance between buy and sell orders, and the only way in which this imbalance can be resolved is with a price change. This price change, that arises from lack of liquidity, will generally be temporary and will be reversed as liquidity returns to the market.
The second reason for the price impact is informational. A large trade attracts the attention of other investors in that asset market because if might be motivated by new information that the trader possesses. Notwithstanding claims to the contrary, investors usually assume, with good reason, that an investor buying a large block is buying in advance of good news and that an investor selling a large block has come into possession of some negative news about the company. This price effect will generally not be temporary, especially when we look at a large number of stocks where such large trades are made. While investors are likely to be wrong a fair proportion of the time on the informational value of large block trades, there is reason to believe that they will be right almost as often.
How large is the price impact?
There is conflicting evidence on how much of a impact large trades have on stock prices. On the one hand, studies of block trades on the exchange floor seem to suggest that markets are liquid and that the price impact is small and is reversed quickly. These studies, however, have generally looked at heavily traded stocks at the New York Stock exchange. On the other hand, there are others who argue that the price impact is likely to be large, especially for smaller and less liquid stocks.
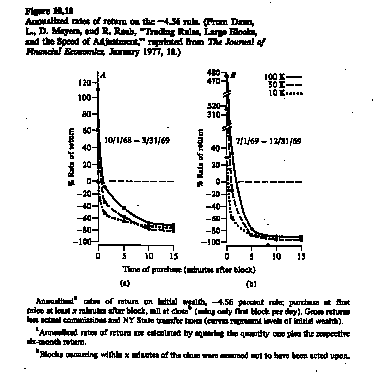
Studies of the price reaction to large block trades on the floor of the exchange conclude that prices adjust within a few minutes to such trades. Dann, Mayers and Rabb examined the speed of the price reaction by looking at the returns an investor could make by buying stock right around the block trade and selling later. They estimated the returns as a function of how many minutes the acquisition took place after the block trade, and found that only trades made within a couple of minutes of the block trade had a chance of making excess returns. (See Figure 12.2) Put another way, prices adjusted to the liquidity effects of the block trade within five minutes of the block. While this may be understated because of the fact that these were block trades on large stocks on the NYSE, it is still fairly strong evidence of the capacity of markets to adjust quickly to imbalances between demand and supply.
Figure 12.2: Returns around Block Trades
These and similar studies suffer from a sampling bias - they tend to look at large block trades in liquid stocks on the exchange floor — they also suffer from another selection bias, insofar as they look only at actual executions. The true cost of market impact arises from those trades that would have been done in the absence of a market impact but were not because of the perception that it would be large. In one of few studies of how large this cost could be, Thomas Loeb collected bid and ask prices from specialists and market makers, at a point in time, for a variety of block sizes. Thus, the differences in the spreads as the block size increases can be viewed as an expected price impact from these trades. Table 12.3 summarizes his findings across stocks, classified by market capitalization:
Table 12.3: Round-Trip Transactions Costs as a Function of Market Capitalization and Block Size
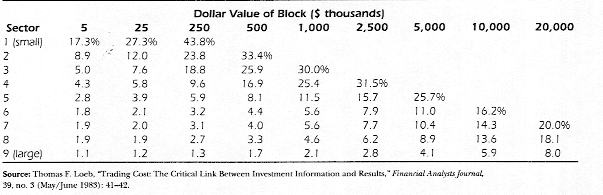
The sectors refer to market capitalization, and show the negative relationship between size and price impact. Note, however the effect of increasing block sizes on expected price impact, within each sector; larger trades elicit much larger price impact than do smaller trades.
The Loeb findings were challenged by Leinweber, who looked at 13,651 equity transactions, totaling about $ 2 billion, by a large corporate pension plan in 1991. In contrast to the positive relationship between block size and the trading costs presented in the Loeb study, he found a very weak relationship between trade size and trading cost. Figure 12.3 presents his findings on the percent trading cost and the size of the trade as a percent of the three-day average trading volume:
Figure 12.3: Percent Trading Costs and Trade Size
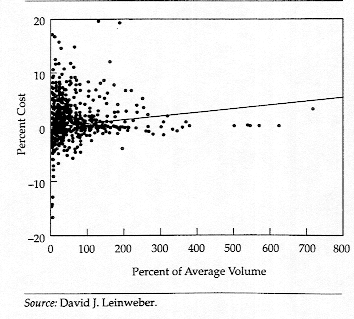
Note the bulge around the smallest trades, which seem to have both the lowest cost and the highest cost trades. Figure 12.4 presents the net trading loss by order size:
Figure 12.4: Net Trading Loss By Order Size
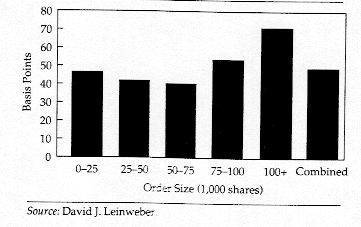
In fact, while smaller trades (<25,000 shares), on average, had lower trading losses than larger trades, they cumulatively accounted for almost 30% of the total trading costs for the fund. Thus, it may be just as important to worry about trading costs on small trades as on large trades, especially given the sheer number of small trades made by many portfolio managers and investors.
Determinants of the Price Impact
Looking at the evidence, the variables that determine that price impact of trading seem to be the same variables that drive the bid-ask spread. That should not be surprising. The price impact and the bid-ask spread are both a function of the liquidity of the market. The inventory costs and adverse selection problems are likely to be largest for stocks where small trades can move the market significantly.
In many real asset markets, the difference between the price at which one can buy the asset and the price at which one can sell, at the same point in time, is a reflection of both the bid-ask spread and the expected price impact of the trade on the asset. Not surprisingly, this difference can be very large in markets where trading is infrequent; in the collectibles market, this cost can amount to more than 20% of the value of the asset.
Role in Investment Strategy
The fact that assets which have high bid-ask spreads also tend to be assets where trading can have a significant price impact makes it even more critical that we examine investment strategies that focus disproportionately in these assets with skepticism. With the price impact, the effect of the size of the portfolio becomes much more critical, since large portfolios beget large trading blocks, which, in turn, have the biggest price impact. Thus, a strategy of investing in low-priced stocks which are not followed by analysts may yield excess returns, even after the bid-ask spread is considered, for a portfolio of $ 25 million but cease to be profitable if that same portfolio becomes $ 500 million.
The final component of trading costs is the opportunity cost of waiting. An investor could reduce the bid-ask spread and price impact costs of trading by trading patiently. If, in fact, there was no cost to waiting, even a large investor could break up trades into small lots and buy or sell large quantities without affecting the price or the spread significantly. There is, however, a cost to waiting. In particular, the price of an asset that an investor wants to buy because he or she believes that it is undervalued may rise while the investor waits to trade, and this, in turn, can lead to one of two consequences. One is that the investor does eventually buy, but at a much higher price, reducing expected profits from the investment. The other is that the price rises so much that the asset is no longer under valued and the investor does not trade at all. A similar calculus applies when an investor wants to sell an asset that he or she thinks is overvalued.
The cost of waiting will depend in great part on the probability that the investor assigns that the price will rise (fall) while he or she waits to buy (sell). We would argue that this probability will be a function of why the investor thinks the asset is under or over valued. In particular, the following factors should affect this probability:
In summary, the cost of waiting is likely to be greatest for short term investment strategies, based upon private information or momentum, in markets with active information gathering. It will be less of an issue for long term investment strategies based upon public information and for contrarian strategies.
The preceding discussion make clear out not only how large the "trading cost" problem is for active money managers, but also how difficult it is to develop a strategy to minimize the collective cost. Actions taken to reduce one type of trading cost (say, the brokerage commission or bid-ask spread) may increase another (for instance, the price impact. Strategies designed to minimize the collective impact of the bid-ask spread and the price impact (such as breaking up trades and using alternative trading routes) may increase the opportunity cost of waiting. In this section, we will examine ways in which trading costs can be managed within the broader construct of maximizing portfolio returns, given an investment philosophy.
Step 1: Develop a coherent investment philosophy and a consistent investment strategy
The first step in managing trading costs is developing and staying with a coherent investment philosophy and strategy. The portfolio managers who pride themselves on style switching and moving from one investment philosophy to another are the ones who bear the biggest burden in terms of transactions costs, partly because style switching increases turnover and partly because it is difficult to develop a trading strategy without a consistent investment strategy.
Step 2: Estimate the cost of waiting given the investment strategy
The second step in the process is determining the cost of waiting for the investment strategy that is being followed. As noted in the previous section, the cost of waiting is likely to small for long-term, contrarian strategies and greater for short-term, information-based and momentum strategies. If the cost of waiting is very high, then the objective has to be minimize this cost, which essentially translates into trading as quickly as one can, even if the other costs of trading increase as a consequence.
Step 3: Look at the alternatives available to minimize transactions costs, given the cost of waiting
Once the cost of waiting has been identified, the investor can consider the third step which is to minimize the effect of the bid-ask spread and the price impact on portfolio returns. While we have talked about trading primarily in terms of trading on the floor of the exchange, there are a number of options that an investor can use to reduce the trading costs. Rose and Cushing make some of the following suggestions to reduce trading costs on a portfolio:
Step 4: Stay within a portfolio size that is consistent with the investment philosophy and trading strategy that has been chosen
While it is tempting to most portfolio managers to view portfolio growth as the fruit of past success, there is a danger that arises from allowing portfolios to become too big. How big is too big? It depends upon both the portfolio strategy that has been chosen, and the trading costs associated with that strategy. While a long-term value investor who focuses well-known, large-capitalization stocks might be able to allow his or her portfolio to increase to almost any size, an investor in small-cap, high growth stocks or emerging market stocks may not have the same luxury, because of the trading costs we have enumerated in the earlier sections.
Step 5: Consider whether your investment strategy is yielding returns that exceed the costs
The ultimate test of an investment strategy lies in whether it earns excess returns after transactions costs. Once an investor has gone through the first four steps, the moment of truth always arrives when the performance of the portfolio is evaluated. If a strategy consistently delivers returns that are lower than the costs associated with implementing the strategy, the investor has one of two choices - he or she can switch to a passive investing approach (such as an index fund) or to a different active investing strategy, with higher expected returns or lower trading costs or both.
Summing Up..
In conclusion, trading costs are an integral part of any investment portfolio and can make the difference between a portfolio that beats the market and one that does not. The overall evidence suggests that trading costs impose a significant drag on portfolio returns, and may explain why active money managers under perform the market. The reason trading costs are large is that they include not just brokerage costs, but also the costs associated with the bid-ask spread, the price impact created by trading and the cost of waiting. The reason they are difficult to control is that actions taken to reduce one component of the trading cost tend to increase the other components.
Trading costs do not impose a uniform burden on all investment strategies. They punish short term, information-based strategies far more than they do long term value-based strategies; they affect strategies that focus on small, less-liquid assets far more than they do strategies that are built around liquid assets. No matter what the strategy, though, it is the portfolio manager’s job to manage trading costs, given the constraints of the strategy, and earn an excess return that covers these costs.