Futures Arbitrage

A futures contract is a contract to buy (and sell) a specified asset at a fixed price in a future time period. There are two parties to every futures contract - the seller of the contract, who agrees to deliver the asset at the specified time in the future, and the buyer of the contract, who agrees to pay a fixed price and take delivery of the asset. If the asset that underlies the futures contract is traded and is not perishable, you can construct a pure arbitrage if the futures contract is mispriced. In this section, we will consider the potential for arbitrage first with storable commodities and then with financial assets and then look at whether such arbitrage is possible.

The Arbitrage Relationships

The basic arbitrage relationship can be derived fairly easily for futures contracts on any asset, by estimating the cashflows on two strategies that deliver the same end result – the ownership of the asset at a fixed price in the future. In the first strategy, you buy the futures contract, wait until the end of the contract period and buy the underlying asset at the futures price. In the second strategy, you borrow the money and buy the underlying asset today and store it for the period of the futures contract. In both strategies, you end up with the asset at the end of the period and are exposed to no price risk during the period – in the first, because you have locked in the futures price and in the second because you bought the asset at the start of the period. Consequently, you should expect the cost of setting up the two strategies to exactly the same. Across different types of futures contracts, there are individual details that cause the final pricing relationship to vary – commodities have to be stored and create storage costs whereas stocks may pay a dividend while you are holding them.

a. Storable Commodities

The distinction between storable and perishable goods is that storable goods can be acquired today at the spot price and stored till the expiration of the futures contract, which is the practical equivalent of buying a futures contract and taking delivery at expiration. Since the two approaches provide the same result, in terms of having possession of the commodity at expiration, the futures contract, if priced right, should cost the same as a strategy of buying and storing the commodity. The two additional costs of the latter strategy are as follows.

(a) Since the commodity has to be acquired now, rather than at expiration, there is an added financing cost associated with borrowing the funds needed for the acquisition now.

Added Interest Cost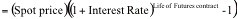

(b) If there is a storage cost associated with storing the commodity until the expiration of the futures contract, this cost has to be reflected in the strategy as well. In addition, there may be a benefit to having physical ownership of the commodity. This benefit is called the convenience yield and will reduce the futures price. The net storage cost is defined to be the difference between the total storage cost and the convenience yield.

If F is the futures contract price, S is the spot price, r is the annualized interest rate, t is the life of the futures contract and k is the net annual storage costs (as a percentage of the spot price) for the commodity, the two equivalent strategies and their costs can be written as follows.

Strategy 1: Buy the futures contract. Take delivery at expiration. Pay $F.

Strategy 2: Borrow the spot price (S) of the commodity and buy the commodity. Pay the additional costs.

(a) Interest cost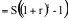

(b) Cost of storage, net of convenience yield = S k t

If the two strategies have the same costs,

F*

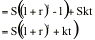
This is the basic arbitrage relationship between futures and spot prices. Note that the futures price does not depend upon your expectations of what will happen to the spot price over time but on the spot price today. Any deviation from this arbitrage relationship should provide an opportunity for arbitrage, i.e., a strategy with no risk and no initial investment, and for positive profits. These arbitrage opportunities are described in Figure 11.1.

This arbitrage is based upon several assumptions. First, investors are assumed to borrow and lend at the same rate, which is the riskless rate. Second, when the futures contract is over priced, it is assumed that the seller of the futures contract (the arbitrageur) can sell short on the commodity and that he can recover, from the owner of the commodity, the storage costs that are saved as a consequence. To the extent that these assumptions are unrealistic, the bounds on prices within which arbitrage is not feasible expand. Assume, for instance, that the rate of borrowing is rb and the rate of lending is ra, and that short seller cannot recover any of the saved storage costs and has to pay a transactions cost of ts. The futures price will then fall within a bound.

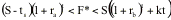
If the futures price falls outside this bound, there is a possibility of arbitrage and this is illustrated in Figure 11.2.

Figure 11.1: Storable Commodity Futures: Pricing and Arbitrage

F* = S ((1+r)t + k t)

____________________________________________________________

If F > F* If F < F*

Time Action Cashflows Action Cashflows

Now: 1. Sell futures contract 0 1. Buy futures contract 0

2. Borrow spot price at riskfree r S 2. Sell short on commodity S

3. Buy spot commodity -S 3. Lend money at riskfree rate -S

At t: 1. Collect commodity; Pay storage cost. -Skt 1. Collect on loan S(1+r)t

2. Deliver on futures contract F 2. Take delivery of futures contract -F

3. Pay back loan -S(1+r)t 3. Return borrowed commodity;

Collect storage costs +Skt

NCF= F-S((1+r)t - kt) > 0 S((1+r)t + kt) - F > 0

Key inputs:

F* = Theoretical futures price r= Riskless rate of interest (annualized)

F = Actual futures price t = Time to expiration on the futures contract

S = Spot price of commodity k = Annualized carrying cost, net of convenience yield (as % of spot price)

Key assumptions

1. The investor can lend and borrow at the riskless rate.

2. There are no transactions costs associated with buying or selling short the commodity.

3. The short seller can collect all storage costs saved because of the short selling.

Figure 11.2: Storable Commodity Futures: Pricing and Arbitrage with Modified Assumptions

Modified Assumptions

1. Investor can borrow at rb (rb > r) and lend at ra (ra < r).

2. The transactions cost associated with selling short is ts (where ts is the dollar transactions cost).

3. The short seller does not collect any of the storage costs saved by the short selling.

______________________________________________________________________________________________________

Fh* = S ((1+rb)t + k t)

Fl* = (S-ts) (1+ra)t

____________________________________________________________

If F > Fh* If F < Fl*

Time Action Cashflows Action Cashflows

Now: 1. Sell futures contract 0 1. Buy futures contract 0

2. Borrow spot price at rb S 2. Sell short on commodity S - ts

3. Buy spot commodity -S 3. Lend money at ra -(S - ts)

At t: 1. Collect commodity from storage -Skt 1. Collect on loan (S-ts)(1+ra)t

2. Delivery on futures contract F 2. Take delivery of futures contract -F

3. Pay back loan -S(1+rb)t 3. Return borrowed commodity;

Collect storage costs 0

NCF= F-S((1+rb)t - kt)> 0 (S-ts) (1+ra)t - F > 0

Fh = Upper limit for arbitrage bound on futures prices Fl = Lower limit for arbitrage bound on futures prices

b. Stock Index Futures

Futures on stock indices have become an important and growing part of most financial markets. Today, you can buy or sell futures on the Dow Jones, the S&P 500, the NASDAQ and the Value Line indices, as well as many indices in other countries. An index future entitles the buyer to any appreciation in the index over and above the index futures price and the seller to any depreciation in the index from the same benchmark. To evaluate the arbitrage pricing of an index future, consider the following strategies.

Strategy 1: Sell short on the stocks in the index for the duration of the index futures contract. Invest the proceeds at the riskless rate. This strategy requires that the owners of the stocks that are sold short be compensated for the dividends they would have received on the stocks.

Strategy 2: Sell the index futures contract.

Both strategies require the same initial investment, have the same risk and should provide the same proceeds. Again, if S is the spot price of the index, F is the futures prices, y is the annualized dividend yield on the stock and r is the riskless rate, the cash flows from the two contracts at expiration can be written.

F* = S (1 + r - y)t

If the futures price deviates from this arbitrage price, there should be an opportunity from arbitrage. This is illustrated in Figure 11.3.

This arbitrage is also conditioned on several assumptions. First, we assume that investors can lend and borrow at the riskless rate. Second, we ignore transactions costs on both buying stock and selling short on stocks. Third, we assume that the dividends paid on the stocks in the index are known with certainty at the start of the period. If these assumptions are unrealistic, the index futures arbitrage will be feasible only if prices fall outside a band, the size of which will depend upon the seriousness of the violations in the assumptions.

Assume that investors can borrow money at rb and lend money at ra and that the transactions costs of buying stock is tc and selling short is ts. The band within which the futures price must stay can be written as:

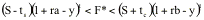
The arbitrage that is possible if the futures price strays outside this band is illustrated in Figure 11.4.

In practice, one of the issues that you have to factor in is the seasonality of dividends since the dividends paid by stocks tend to be higher in some months than others. Figure 11.5 graphs out dividends paid as a percent of the S&P 500 index on U.S. stocks in 2000 by month of the year.

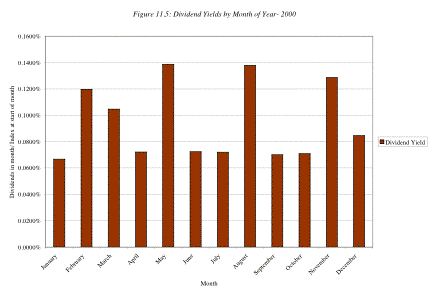
Thus, dividend yields seem to peak in February, May, August and November. An index future coming due in these months is much more likely to be affected by dividend yields especially as maturity draws closer.

Figure 11.3: Stock Index Futures: Pricing and Arbitrage

F* = S (1+r-y)t

____________________________________________________________

If F > F* If F < F*

Time Action Cashflows Action Cashflows

Now: 1. Sell futures contract 0 1. Buy futures contract 0

2. Borrow spot price of index at riskfree r S 2. Sell short stocks in the index S

3. Buy stocks in index -S 3. Lend money at riskfree rate -S

At t: 1. Collect dividends on stocks S((1+y)^t-1) 1. Collect on loan S(1+r)t

2. Delivery on futures contract F 2. Take delivery of futures contract -F

3. Pay back loan -S(1+r)t 3. Return borrowed stocks;

Pay foregone dividends - S((1+y)^t-1)

NCF= F-S(1+r-y)t > 0 S (1+r-y)t - F > 0

Key inputs:

F* = Theoretical futures price r= Riskless rate of interest (annualized)

F = Actual futures price t = Time to expiration on the futures contract

S = Spot level of index y = Dividend yield over lifetime of futures contract as % of current index level

Key assumptions

1. The investor can lend and borrow at the riskless rate.

2. There are no transactions costs associated with buying or selling short stocks.

3. Dividends are known with certainty.

Figure 11.4: Stock Index Futures: Pricing and Arbitrage with modified assumptions

Modified Assumptions

1. Investor can borrow at rb (rb > r) and lend at ra (ra < r).

2. The transactions cost associated with selling short is ts (where ts is the dollar transactions cost) and the transactions cost associated with buying the stocks in the index is tc.

______________________________________________________________________________________________________

Fh* = (S+tc) (1+r_b-y)t

Fl* = (S-ts) (1+r_a-y)t

____________________________________________________________

If F > Fh* If F < Fl*

Time Action Cashflows Action Cashflows

Now: 1. Sell futures contract 0 1. Buy futures contract 0

2. Borrow spot price at rb S+tc 2. Sell short stocks in the index S - ts

3. Buy stocks in the index -S-tc 3. Lend money at ra -(S - ts)

At t: 1. Collect dividends on stocks S((1+y)^t-1) 1. Collect on loan (S-ts)(1+ra)t

2. Delivery on futures contract F 2. Take delivery of futures contract -F

3. Pay back loan -(S+tc)(1+rb)t 3. Return borrowed stocks;

Pay foregone dividends -S((1+y)^t-1)

NCF= F-(S+tc) (1+r_b-y)^t > 0 (S-ts) (1+r_a-y)t - F > 0

Fh = Upper limit for arbitrage bound on futures prices Fl = Lower limit for arbitrage bound on futures prices

c. Treasury Bond Futures

The treasury bond futures traded on the CBOT require the delivery of any government bond with a maturity greater than fifteen years, with a no-call feature for at least the first fifteen years. Since bonds of different maturities and coupons will have different prices, the CBOT has a procedure for adjusting the price of the bond for its characteristics.

The conversion factor itself is fairly simple to compute and is based upon the value of the bond on the first day of the delivery month, with the assumption that the interest rate for all maturities equals 8% per annum (with semi-annual compounding). For instance, you can compute the conversion factor for a 9% coupon bond with 18 years to maturity.. Working in terms of a $100 face value of the bond, the value of the bond can be written as follows, using the interest rate of 8%.

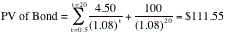
The conversion factor for this bond is 109.90. Generally speaking, the conversion factor will increase as the coupon rate increases and with the maturity of the delivered bond.

This feature of treasury bond futures, i.e., that any one of a menu of treasury bonds can be delivered to fulfill the obligation on the bond, provides an advantage to the seller of the futures contract. Naturally, the cheapest bond on the menu, after adjusting for the conversion factor, will be delivered. This delivery option has to be priced into the futures contract. There is an additional option embedded in treasury bond futures contracts that arises from the fact that the T.Bond futures market closes at 2 p.m., whereas the bonds themselves continue trading until 4 p.m. The seller does not have to notify the clearing house until 8 p.m. about his intention to deliver. If bond prices decline after 2 p.m., the seller can notify the clearing house of intention to deliver the cheapest bond that day. If not, the seller can wait for the next day. This option is called the wild card play.

The valuation of a treasury bond futures contract follows the same lines as the valuation of a stock index future, with the coupons of the treasury bond replacing the dividend yield of the stock index. The theoretical value of a futures contract should be –

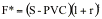
where,

F* = Theoretical futures price for Treasury Bond futures contract

S = Spot price of Treasury bond

PVC = Present Value of coupons during life of futures contract

r = Riskfree interest rate corresponding to futures life

t = Life of the futures contract

If the futures price deviates from this theoretical price, there should be the opportunity for arbitrage. These arbitrage opportunities are illustrated in Figure 11.6.

This valuation ignores the two options described above - the option to deliver the cheapest-to-deliver bond and the option to have a wild card play. These give an advantage to the seller of the futures contract and should be priced into the futures contract. One way to build this into the valuation is to use the cheapest deliverable bond to calculate both the current spot price and the present value of the coupons. Once the futures price is estimated, it can be divided by the conversion factor to arrive at the standardized futures price.

Figure 11.6: Treasury Bond Futures: Pricing And Arbitrage

F* = (S - PVC) (1+r)t

____________________________________________________________

If F > F* If F < F*

Time Action Cashflows Action Cashflows

Now: 1. Sell futures contract 0 1. Buy futures contract 0

2. Borrow spot price of bond at riskfree r S 2. Sell short treasury bonds S

3. Buy treasury bonds -S 3. Lend money at riskfree rate -S

Till t: 1. Collect coupons on bonds; Invest PVC(1+r)^t 1. Collect on loan S(1+r)t

2. Deliver the cheapest bond on contract F 2. Take delivery of futures contract -F

3. Pay back loan -S(1+r)t 3. Return borrowed bonds;

Pay foregone coupons w/interest - PVC(1+r)^t

NCF= F-(S-PVC)(1+r)t > 0 (S-PVC) (1+r)t - F > 0

Key inputs:

F* = Theoretical futures price r= Riskless rate of interest (annualized)

F = Actual futures price t = Time to expiration on the futures contract

S = Spot level of treasury bond PVC = Present Value of Coupons on Bond during life of futures contract

Key assumptions

1. The investor can lend and borrow at the riskless rate.

2. There are no transactions costs associated with buying or selling short bonds.

d. Currency Futures

In a currency futures contract, you enter into a contract to buy a foreign currency at a price fixed today. To see how spot and futures currency prices are related, note that holding the foreign currency enables the investor to earn the risk-free interest rate (R_f) prevailing in that country while the domestic currency earn the domestic riskfree rate (R_d). Since investors can buy currency at spot rates and assuming that there are no restrictions on investing at the riskfree rate, we can derive the relationship between the spot and futures prices. Interest rate parity relates the differential between futures and spot prices to interest rates in the domestic and foreign market.

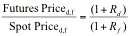
where Futures Price_d,f is the number of units of the domestic currency that will be received for a unit of the foreign currency in a forward contract and Spot Price_d,f is the number of units of the domestic currency that will be received for a unit of the same foreign currency in a spot contract. For instance, assume that the one-year interest rate in the United States is 5% and the one-year interest rate in Germany is 4%. Furthermore, assume that the spot exchange rate is $0.65 per Deutsche Mark. The one-year futures price, based upon interest rate parity, should be as follows:

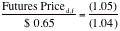
resulting in a futures price of $0.65625 per Deutsche Mark.

Why does this have to be the futures price? If the futures price were greater than $0.65625, say $0.67, an investor could take advantage of the mispricing by selling the futures contract, completely hedging against risk and ending up with a return greater than the riskfree rate. The actions the investor would need to take are summarized in Table 11.1, with the cash flows associated with each action in brackets next to the action.

Table 11.1: Arbitrage when currency futures contracts are mispriced

Forward Rate Mispricing	Actions to take today	Actions at expiration of futures contract
If futures price > $0.65625 e.g. $0.67	1. Sell a futures contract at $0.67 per Deutsche Mark. ($0.00) $ 0.00 2. Borrow the spot price in the U.S. domestic markets @ 5%. (+$0.65) + $ 0.65 3. Convert the dollars into Deutsche Marks at spot price. (-$0.65/+1 DM) - $ 0.65/+ 1 DM 4. Invest Deustche Marks in the German market @ 4%. (-1 DM) - 1 DM	1. Collect on Deutsche Mark investment. (+1.04 DM) 1.04 DM 2. Convert into dollars at futures price. (-1.04 DM/ +$0.6968) -1.04 DM to + $ 0.6968 3. Repay dollar borrowing with interest. (-$0.6825) Profit = $0.6968 - $0.6825 = $ 0.0143
If futures price < $0.65625 e.g. $0.64	1. Buy a futures price at $0.64 per Deutsche Mark. ($0.00) $ 0.00 2. Borrow the spot rate in the German market @4%. (+1 DM) + 1 DM 3. Convert the Deutsche Marks into Dollars at spot rate. (-1 DM/+$0.65) - 1 DM/ $ 0.65 4. Invest dollars in the U.S. market @ 5%. (-$0.65) - $ 0.65	1. Collect on Dollar investment. (+$0.6825) $ 0.6825 2. Convert into dollars at futures price. (-$0.6825/1.0664 DM) - $ 0.6825 /+1.0664 DM 3. Repay DM borrowing with interest. (1.04 DM) Profit = 1.0664-1.04 = 0.0264 DM - 1.04 DM + 0.0264 DM

The first arbitrage of Table 11.1 results in a riskless profit of $0.0143, with no initial investment. The process of arbitrage will push down futures price towards the equilibrium price.

If the futures price were lower than $0.65625, the actions would be reversed, with the same final conclusion. Investors would be able to take no risk, invest no money and still end up with a positive cash flow at expiration. In the second arbitrage of Table 34.3, we lay out the actions that would lead to a riskless profit of .0164 DM.