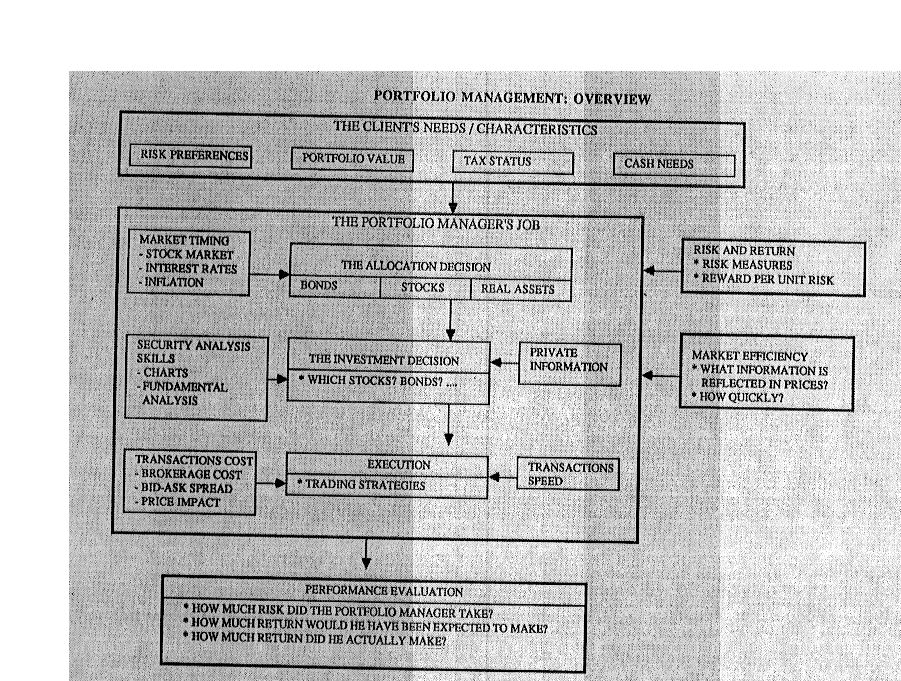

The trade off between Risk and Return
Most, if not all, investors are risk averse
To get them to take more risk, you have to offer higher expected returns
Conversely, if investors want higher expected returns, they have to be willing to take more risk.
Ways of evaluating risk
Most investors do not know have a quantitative measure of how much risk that they want to take
Traditional risk and return models tend to measure risk in terms of volatility or standard deviation
In the mean-variance world, variance is the only measure of risk. Investors given a choice between tow investments with the same expected returns but different variances, will always pick the one with the lower variance.
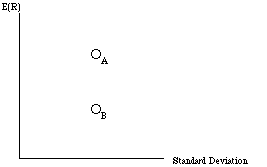
Illustration 1: Calculation of expected returns/standard deviation using historical returns
|
|
|
|
|
|
The Home Depot |
| ||||||
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
| ||||||
|
|
$ 32.25 |
|
|
$ 8.13 |
|
| ||||||
|
|
$ 28.66 |
$ 0.95 |
|
$ 12.88 |
$ 0.04 |
| ||||||
|
|
$ 38.25 |
$ 1.00 |
|
$ 33.66 |
$ 0.05 |
| ||||||
|
|
$ 42.75 |
$ 1.00 |
|
$ 50.63 |
$ 0.07 |
| ||||||
|
|
$ 52.42 |
$ 1.00 |
|
$ 39.50 |
$ 0.11 |
| ||||||
|
|
$ 51.00 |
$ 1.00 |
|
$ 46.00 |
$ 0.15 |
| ||||||
|
Average |
|
|
|
|
|
| ||||||
|
Standard Deviation |
|
|
|
|
| |||||||
Concept Check:
mportfolio = wA mA + (1 - wA) mB
s2portfolio = wA2 s2A + (1 - wA)2 s2B + 2 wA wB rAB sA sB
where
wA = Proportion of the portfolio in asset A
The last term in the variance formulation is sometimes written in terms of the covariance in returns between the two assets, which is
sAB = rAB sA sB
Illustration 2: Extending the two-asset case - GE and The Home Depot
Step 1: Use historical data to estimate average returns and standard deviations in returns for the two investments.
|
|
|
|
|
General Electric |
13.46% |
18.42% |
|
The Home Depot |
53.26% |
68.50% |
Step 2: Estimate the correlation and covariance in returns between the two investments using historical data.
|
|
|
|
|
|
|
|
|
|
|
0.04686 |
0.00309 |
(0.01203) |
|
|
|
|
0.05518 |
1.17786 |
0.25494 |
|
|
|
|
0.00008 |
0.00071 |
(0.00024) |
|
|
|
|
0.01322 |
0.56265 |
(0.08625) |
|
|
|
|
0.02034 |
0.13265 |
0.05194 |
|
|
|
|
0.13568 |
1.87696 |
0.20835 |
Variance in GE Returns = 0.13568/4 = 0.0339 Standard Deviation in GE Returns = 0.03390.5 = 0.1842
Variance in HD Returns = 1.87696/4 = 0.4692 Standard Deviation in HD Returns = 0.46920.5 = 0.6850
Covariance between GE and The Home Depot Returns = 0.20835/4 = 0.0521
Correlation between GE and The Home Depot Returns =rGH = sGH /sG sH = 0.0521/(0.1842*0.6850) = 0.4129
Step 3: Compute the expected returns and variances of portfolios of the two securities using the statistical parameters estimates above ñ
Consider, for instance, a portfolio composed of 50% in GE and 50% in The Home Depot ñ
Average Return of Portfolio = 0.5 (13.46%) + 0.5 (53.26%) =
Variance of Portfolio = (0.5)2 (18.42%)2 + (0.5)2 (68.50%)2 + 2 (0.5) (0.5) (0.4129) (18.42%) (68.50%) = 1518%
Standard Deviation of Portfolio = 38.96%
From Two Assets To Three Assets to n Assets
The variance of a portfolio of three assets can be written as a function of the variances of each of the three assets, the portfolio weights on each and the correlations between pairs of the assets. The variance can be written as follows -
sp2= wA2 s2A + wB2 s2B + wC2 s2C+ 2 wA wB rAB sA sB+ 2 wA wC rAC sA sC+ 2 wB wC rBC sB sC
where
wA,wB,wC = Portfolio weights on assets
s2A ,s2B ,s2C = Variances of assets A, B, and C
rAB , rAC , rBC = Correlation in returns between pairs of assets (A&B, A&C, B&C)
![]()
where n is the number of assets in the portfolio
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Most Investors do not measure their risk preferences in terms of standard deviation
For other investors, risk has to be assessed by using
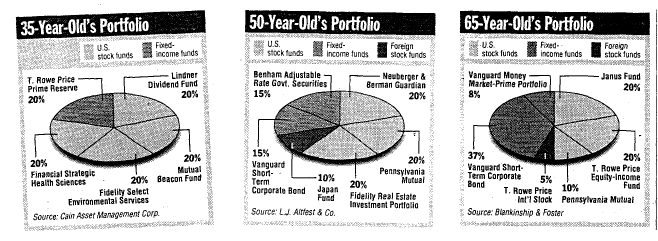
General Propositions:
As investors age, there will be a general increase in risk aversion, leading to greater allocation to safer asset classes.
Stocks
Bonds
Market Returns
$ 534.46
$ 17.30
After Transactions Cost
$ 354.98
$ 11.47
After Income Taxes
$ 161.55
$ 4.91
After Capital Gains Taxes
$ 113.40
$ 4.87
After Inflation
$ 16.10
$ 0.69
Transactions Costs: 0.5% a year;
Income taxes: at 28%; Capital Gains at 28% every 20 years;
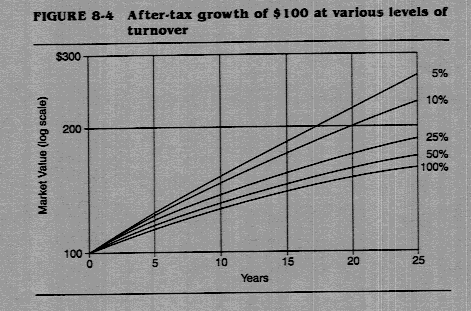
- What is a long time horizon?
- Determinants of time horizon
* Age
* Level of Income
* Stability of Income
* Cash Requirements
- Time Horizon and Asset Choice
Proposition: The cost of keeping funds in near-cash investments increases with the time horizon of the investor.
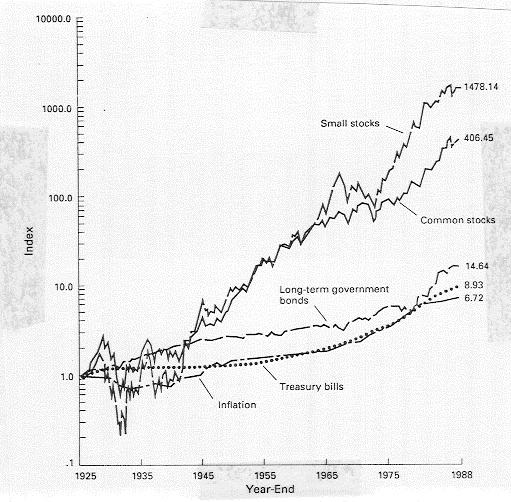
|
|
|
|
|
Objective Function |
Maximize Expected Return
|
Minimize return variance
|
|
Constraint |
|
|
where,
s2 = Investor's desired level of variance
E(R) = Investor's desired expected returns
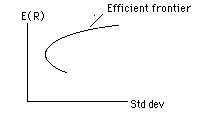
The portfolios that emerge from this process are called Markowitz portfolios. These portfolios are considered efficient, because they maximize expected returns given the standard deviation, and the entire set of portfolios is referred to as the Efficient Frontier. Graphically, these portfolios are shown on the expected return/standard deviation dimensions in figure 5.7 -
|
Asset Class |
Mean |
Standard deviation |
|
U.S. stocks |
12.50% |
16.50% |
|
U.S. bonds |
6.50% |
5.00% |
|
Foreign Stocks |
15.00% |
26.00% |
|
Real Estate |
11.00% |
12.50% |
|
|
U.S. Stock |
U.S. Bonds |
Foreign Stocks |
Real Estate |
|
U.S. Stocks |
|
|
|
|
|
U.S. Bonds |
|
|
|
|
|
Foreign Stocks |
|
|
|
|
|
Real Estate |
|
|
|
|
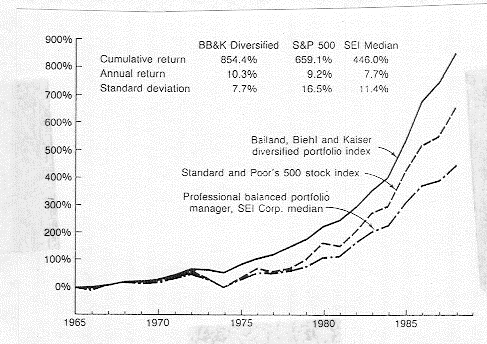
The objective is to create a portfolio to take advantage of 'forecasted' market movements, up or down. Strategies could include:
* Shifting from (to) overvalued asset classes to (from) undervalued asset classes if you expect the market to go up (down).
* Buying calls (puts) or buying (selling) futures on a market if you expect the market to go up (down).
Assumption: You can forecast market movements
Advantage: If you can forecast market movements, the rewards are immense.
Disadvantage: If you err, the costs can be significant.
Index funds are created by holding stocks in a wider index in proportion to their market value. No attempt is made to trade on a frequent basis to catch market upswings or downswings or select 'good' stocks.
Assumptions: Markets are efficient. Attempts to time the market and pick good stocks are expensive and do not provide reasonable returns. Holding a well diversified portfolio eliminates unsystematic risk.
Advantages:
Transactions costs are minimal as is the cost of searching for
information.
B. Markowitz Portfolio: A Markowitz efficient portfolio is created by searching through all possible combinations of the universe of securities to find that combination that maximizes expected return for any given level of risk.
Assumptions: The portfolio manager can identify the inputs (mean, variance, covariance) to the model correctly and has enough computer capacity to run through the optimization exercise.
Advantages: If historical data is used, the process is inexpensive and easily mechanised.
Disadvantages: The model is only as good as its inputs.
The objective is to use the skills of your security analysts to select stocks that will outperform the market, and create a portfolio of these stocks. The security selection skills can take on several forms.
(1) Technical Analysis, where charts reveal the direction of future price movements
(2) Fundamental Analysis, where public information is used to pick undervalued stocks
(3) Access to private information, which enables the analyst to pinpoint mis-valued securities.
Assumption: Your stock selection skills help you make choices which, on average, beat the market.
Inputs: The model will vary with the security selection model used.
Advantage: If there are systematic errors in market valuation andyour model can spot these errors, the portfolio will outperform others in the market.
Disadvantage: If your security selection does not pay off, you have expended time and resources to earn what another investor could have made with random selection.Security Selection strategies vary widely and can lead to contradictory recommendations..
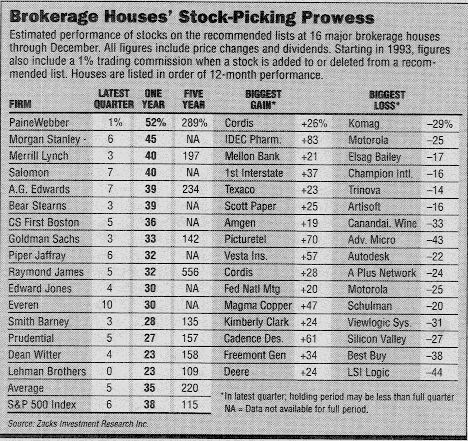
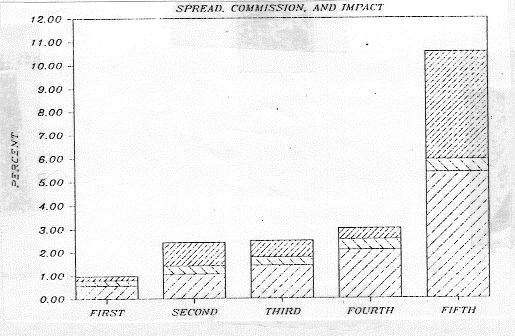
Maximize: Speed of Execution
Subject to: Cost of execution < Excess returns from strategy
Minimize: Cost of Execution
Subject to: Speed of execution < Specified time period.
* Who should measure performance?
Performance measurement has to be done either by
the client or by an objective third party on the basis of agreed upon
criteria. It should not be done by the portfolio manager.
* How often should performance be measured?
The frequency of portfolio evaluation should be a function of both the time horizon of the client and the investment philosophy of the portfolio manager. However, portfolio measurement and reporting of value to clients should be done on a frequent basis.
* How should performance be measured?
I. Market Indices (No adjustment for risk): There are some who do not like models for risk and return and prefer comparison to broad market indices (S&P 500, NYSE composite, ..)
The limitation of this approach is that it does not explicitly control for risk. Thus, an advantage is given to risky funds and money managers.
Tracking Error as a Measure of Risk
Tracking error measures the difference between a portfolioís return and its benchmark index. Thus portfolios that deliver higher returns than the benchmark
II. Against other portfolio managers
In some cases, portfolio managers are measured against other portfolio managers who have similar objective functions. Thus, a growth fund manager may be measured against all growth fund managers.
III. Risk-Adjusted Models
A. The CAPM: The
capital asset pricing model provides a simple and intuitive measure
for measuring performance. It compares the actual returns made by a
portfolio manager with the returns he should have made, given both
market performance during the period and the beta of the portfolio
created by the manager.
Abnormal Return = Actual Return - Expected Return
> 0: Outperformed
< 0: Underperformed
where,
Actual Return = Returns on the portfolio (including dividends)
Expected Return = Riskfree rate at the start of the period + Beta of portfolio * (Actual return on market during the period - Riskfree Rate)
This abnormal return is called Jensen's Alpha. It can also be computed by regressing the returns on the portfolio against a market index, and then comparing the intercept to Rf (1- Beta).
Variants: Define Rp to be the return on the portfolio and Rm to be the return on the market.
Treynor Index = (Rp - Rf)/ Beta of the portfolio
> (Rm - Rf) : Outperformed
< (Rm - Rf) : Underperformed
Sharpe Index = (Rp - Rf)/ Variance of the portfolio
> (Rm - Rf)/sm : Outperformed
< (Rm - Rf)/sm : Underperformed
Information Ratio = Jensenís alpha / Unsystematic Risk
> 0: Outperformed the market
< 0 : Underperformed
Performance Attribtion
This analysis can be carried one step forward, and the overall performance of a money manager can be decomposed into ìmarket timingî and ìsecurity selectionî components.
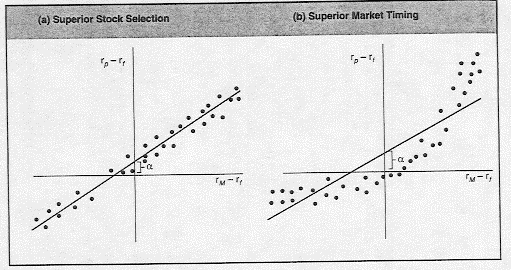
In some cases, better estimates of market timing can be obtained by fitting a quadratic curve to actual returns.
![]()
where c is a measure of the market timing ability of a fund (money manager).
B. The APT: The arbitrage pricing theory defines the expected return in terms of statistical factors (instead of just the market as in the CAPM). A beta is defined relative to each factor.
C. Multi-Index Models: Multi-index models allow the performance evaluator to bring in economic factors that may influence expected returns.
* Window Dressing and other Phenomena that cloud measurement
1. Marking up the merchandise (thinly traded stocks)
2. Tricking the technicians (stocks with breakout points)
3. Playing catch up (Buying hot stocks just before evaluation)
4. Dumping the losers just before evaluation