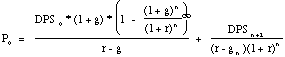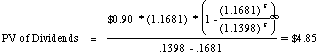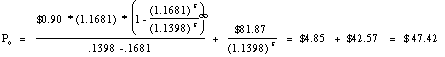I. THE STABLE GROWTH DDM: GORDON GROWTH MODEL
The Model:
Value of Stock = DPS1 / ( r - g)
where DPS1 = Expected Dividends one year from now
r = Required rate of return for equity investors
g = Annual Growth rate in dividends forever
A BASIC PREMISE
- This infinite growth rate cannot exceed the growth rate for the
overall economy (GNP) by more than a small amount (1-2%)
Estimate for the US
Upper end: Long term inflation rate (5%) + Growth rate in real
GNP (3%) =8%
Lower end: Long term inflation rate (3%) + Growth rate in real
GNP (2%) = 5%
- If the company is a multinational, the real growth rate will be
the growth rate of the world economy, whch is about one percent
higher.
- The inflation rate used should be consistent with the currency
being used in the valuation.
WORKS BEST FOR:
- firms with stable growth rates
- firms which pay out dividends that are high and approximate FCFE.
- firms with stable leverage.
Some obvious candidates for the Gordon Growth Model
- Regulated Companies, such as utilities, because
- their growth rates are constrained by geography and population
to be close to the growth rate in the economy in which they operate.
- they pay high dividends, largely again as a function of history
- they have stable leverage (usually high)
- Large financial service companies, because
- their size makes its unlikely that they will generate extraordinary
growth
- Free cash flows to equity are difficult to compute
- they pay large dividends
- they generally do not have much leeway in terms of changing leverage
- Real estate investment trusts, because
- they have to pay out 95% of their earnings as dividends
- they are constrained in terms of invesment policy and cannot grow
at high rates.
Applications: To stocks
Illustration 1: To a utllity: Con Edison - Electrical Utility
(North East United States)
Rationale for using the model
- The firm is in stable growth; based upon size and the area that
it serves. Its rates are also regulated; It is unlikely that the
regulators will allow profits to grow at extraordinary rates.
- The beta is 0.75 and has been stable over time.
- The firm is in stable leverage.
- The firm pays out dividends that are roughly equal to FCFE.
Average Annual FCFE between 1991 and 1995 = $480 million
Average Annual Dividends between 1991 and 1995 = $ 461 million
Dividends as % of FCFE = 96.04%
Background Information
Earnings per share in 1995 = $ 2.95
Dividend Payout Ratio in 1995 = 69.15%
Dividends per share in 1995 = $2.04
Expected Growth Rate in Earnings and Dividends = 5%
Con Ed Beta = 0.75
Cost of Equity = 6% + 0.75*5.5% = 10.13%
Value of Equity = $2.04 *1.05 / (.1013 -.05) = $ 41.80
Con Ed was trading for $ 30 on the day of this analysis. (January
1996)
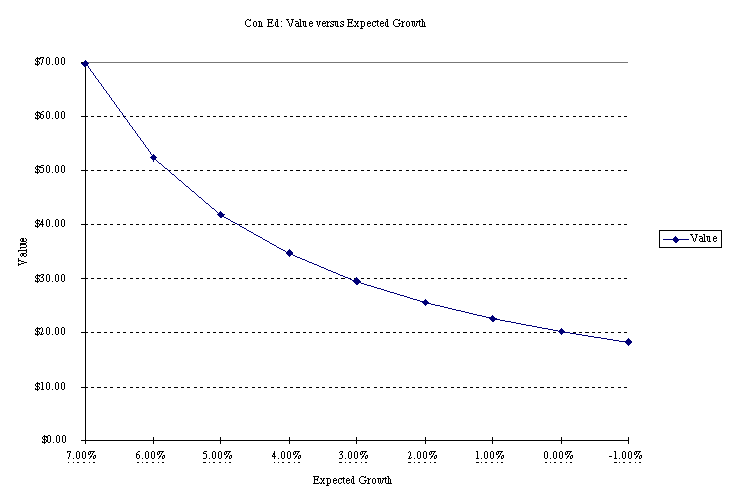
What growth rate would Con Ed have to attain the justify the current
stock price?
The following table estimates value as a function of the expected
growth rate (assuming a beta of 0.75 and current dividends per
share of $2.04).
Solving for the expected growth rate that provides the current
price,
$30.00 = 2.04 (1+g) /(.1013-g)
Solving for g,
g = (.1013*30-2.04)/ (30.00+2.04) = 3.12 %
The growth rate in earnings and dividends would have to be 3.12%
a year to justify the stock price of $30.00.
Illustration 2: To a financial service firm: J.P. Morgan
A Rationale for using the Gordon Growth Model
- As a financial service firm in an extremely competitive environment,
it is unlikely that J.P. Morganís earnings are going to grow much
faster than the economy over the long term. Allowing for expansion,
the expected growth rate used is 7%.
- As a financial service firm, free cash flows to equity are difficult
to estimate. Hence, the dependence on dividends.
- The leverage of financial service firms is high and unlikely to
change over time.
Background Information
Current Earnings per share = $ 6.30
Current Dividend Payout Ratio = 47.62%
Dividends per share = $ 3.00
Expected Growth Rate in Earnings and Dividends = 7%
Stock Beta = 1.15
Cost of Equity = 6% + 1.15 *5.5% = 12.33%
Value of Equity = $3.00 *1.07 / (.1233 -.07) = $ 60.23
J.P. Morgan was trading for $ 80 on the day of this analysis.
(January 1996)
Notes of Concern
- The beta is high for a stable growth firm. It reflects the additional
risk that many financial service firms have encountered and exposed
themselves to in the last few years.
Illustration 3: To the overall market: S&P 500 Index on January
1, 1996
- The average dividend yield (Dividends/ Price) for stocks in the
index at the end of 1995 was 2.32%.
- The level of the index on January 1, 1996 was 611.83.
- Using the T.Bond rate of 6.00% and an expected growth rate in
the nominal GNP of 6%, the level of the index can be obtained
from the Gordon Growth model:
Dividends per share in year 0 = 2.32% of 611.83 = $ 14.19
Infinite growth rate = 6%
Required return of return for equity investors = 6.00% + 1 * 5.5%
= 11.50%
Intrinsic Value of the market = 14.19 * 1.06 / (.115 - .06) =
273.57
Scary! So what are we missing?
- Maybe dividend yields do not reflect the capacity of firms to
buy back stock. With stock buybacks, this measure rises to about
3% of the overall index.
- The risk premium may be trending down, reflecting
- the greater willingness of investors to go with the flow - take
losses and continue in the market, rather than panic
- the greater flow of cash into pension funds
- other paradigm shifts
- With a 3% dividend yield and a 3.5% premium, you can arrive at
an index level of 524.43.
II. TWO-STAGE GROWTH MODEL WITH INFINITE GROWTH RATE AT END
The Model:
- The model is based upon two stages of growth, an extraordinary
growth phase that lasts n years, and a stable growth phase that
lasts forever after that:
Extraordinary growth rate: g% each year for n years Stable growth:
gn forever
|____________________________________________|____________________>
- Value of the Stock = PV of Dividends during extraordinary phase
+ PV of terminal price

where
DPSt = Expected dividends per share in year t
r = Required rate of return
Pn= Price at the end of year n
gn= Growth rate forever after year n
- In the case where the extraordinary growth rate (g) and payout
ratio are the same for the first n years, this formula can be
simplifed as follows:
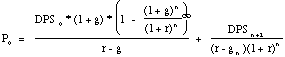
This simplifies calculations because it does not require the estimation
of dividends each year for the first n years.
Calculating the terminal price
- The growth rate for the Gordon Growth Rate model (within 2% of
growth rate in nominal GNP) apply here as well.
- The payout ratio has to be consistent with the estimated growth
rate. If the growth rate is expected to drop significantly after
year n, the payout ratio should be higher. This can be estimated
in one of two ways ñ
Stable Period Payout ratio = 1- b = 1 - (g / (ROA + D/E (ROA -
i (1-t))) = 1 - g/ROE
where the inputs for this equation will be for the stable growth
period.
Stable Period Payout Ratio = Average Payout Ratio for other stable
firms (40-70% depending on industry: See Industry Average Table)
Works best for:
- firms where the growth rate is not yet stable, but is moderating
- firms which pay out dividends that roughly approximate FCFE (or)
FCFE cannot be estimated easily.
Illustration 4: Valuing a firm with the two-stage dividend discount
model::American Express
A Rationale for using the Model
- Why two-stage? While American Express is a large financial service firm in a
competitive market place, normally not a candidate for above-stable
growth, it has gone through an extended period of depressed earnings
. It is expected that the recovery in earnings will create higher
growth over the next five years.
- Why dividends? As a financial service firm, free cash flows to equity are difficult
to estimate.
- Leverage is stable.
Background Information
- Current Earnings / Dividends
- Earnings per share in 1995 = $3.10
- Dividends per share in 1995 = $ 0.90
- Inputs for the High Growth Period
Length of the High Growth Period = 5 years
Beta during High Growth Period = 1.45
Cost of Equity during High Growth Period = 6.0% + 1.45 (5.5%)
= 13.98%
- Return on Assets during high growth period = 14.56% (this was
the 1995 return on assets)
- Dividend Payout Ratio = 29.03%
- Debt/Equity Ratio = 100% (slightly higher than the current debt/equity
ratio of 92.14%)
- Interest rate on debt = 8.50% (Tax Rate = 36%)
Expected Growth Rate = b ( ROA + D/E (ROA - i (1-t)) = 0.7097
(14.56% + 1 (14.56% - 8.50% (1-.36))) = 16.81%
- Inputs for the Stable Growth
- Expected Growth Rate = 6%
- Beta during stable growth phase = 1.10 : Cost of Equity = 6.00%
+ 1.1 (5.5%) = 12.05%
- The ROA is expected to drop to 12.50%; D/E Ratio and interest
rate are assumed to remain unchanged during the stable growth
period.
Stable Payout Ratio = 1 - g / ( ROA + D/E (ROA - i (1-t)) = 1
- .06 / (12.50% + 1 (12.50% - 8.50% (1-.36))) = 69.33%
Estimating the value:
- The first component of value is the present value of the expected
dividends during the high growth period. Based upon the current
earnings ($3.10), the expected growth rate (16.81%) and the expected
dividend payout ratio (29.03%), the expected dividends can be
computed for each year in the high growth period.
|
Year
|
EPS
|
DPS
|
Present Value
|
|
1
|
$3.62
|
$1.05
|
$0.92
|
|
2
|
$4.23
|
$1.23
|
$0.95
|
|
3
|
$4.94
|
$1.43
|
$0.97
|
|
4
|
$5.77
|
$1.68
|
$0.99
|
|
5
|
$6.74
|
$1.96
|
$1.02
|
Cumulative Present Value of Dividends (@13.98%) = $0.92 + $ 0.95+
$ 0.97 + $ 0.99 + $ 1.02 = $ 4.85
The present value of the dividends can also be computed in short
hand using the following computation:
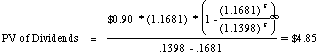
The price at the end of the high growth phase (end of year 5),
can be estimated using the constant growth model.
Terminal price = Expected Dividends per sharen+1 / (r - gn)
Expected Earnings per share6 = 3.10 *1.16815*1.06 = $ 7.15
Expected Dividends per share6 = $7.15 * 0.6933 = $ 4.95
Terminal price = $ 4.95 /(.1205 -.06) = $ 81.87
The present value of the terminal price can be then written as
-
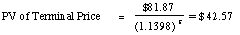
The cumulated present value of dividends and the terminal price
can then be calculated as follows:
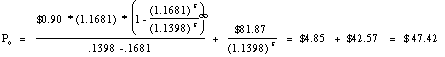
American Express was trading at $40.00 in February 1996, at the
time of this analysis.
THE VALUE OF GROWTH

|_______________________________| |_____________________| |_________|
Extraordinary Growth Stable Growth Assets in place
where
DPSt = Expected dividends per share in year t
r = Required rate of return
Pn= Price at the end of year n
gn= Growth rate forever after year n
Value of extraordinary growth = Value of the firm with extraordinary
growth in first n years - Value of the firm as a stable growth
firm
Value of stable growth = Value of the firm as a stable growth
firm - Value of firm with no growth
Assets in place = Value of firm with no growth
Illustration 5: An Illustration of the value of growth: American
Express
Consider the example of American Express in February 1996,
Value of the assets in place = Current EPS * Payout ratio / r
= $3.10 * 0.2903 / .1205 = $ 7.47
- The discount rate from the stable growth phase is used for this
calculation.
Value of stable growth = Current EPS * Payout ratio * (1+gn)/(r-gn)-
$ 7.47
= ($3.10* 0.2903 *1.06)/(.1205 -.06) - $ 7.47 = $ 8.30
Value of extraordinary growth = $ 47.42 - (7.47+8.30) = $ 31.65
The Determinants of the Value of Growth
- Length of the high growth period
- Extent of the extraordinary growth
- Costs of higher growth , i.e., how much risk is added and how
much cash is drained as a consequence.
III. THREE-STAGE DIVIDEND DISCOUNT MODEL
The Model

- The value of the stock is then the present value of expected dividends
during the high growth and the transitional periods, and of the
terminal price at the start of the final stable growth phase.
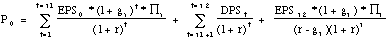
High growth phase Transition Stable growth phase
where,
EPSt = Earnings per share in year t
DPSt = Dividends per share in year t
ga= Growth rate in high growth phase (lasts n1 periods)
gn= Growth rate in stable phase
Pa= Payout ratio in high growth phase
Pn= Payout ratio in stable growth phase
r = Required rate of return on equity
Works best for:
It is best suited for firms which are
- paying out and plan to continue paying dividends which are roughly
equal to FCFE
- growing at
- an extraordinary rate now and are expected to maintain this rate
for an initial period,
- after which the differential advantage of the firm is expected
to deplete leading to gradual declines in the growth rate
- to a stable growth rate.
- in stable leverage
Illustration 6 : Valuing with the Three-stage DDM model: The Home
Depot
A Rationale for using the Three-Stage Dividend Discount Mode;
- Why three-stage? The Home Depot is still in very high growth. Analysts project
that its earnings per share will grow at 36% for the next five
years.
- Why dividends? The firm has had a track record of paying out dividends that
roughly approximate FCFE
- The financial leverage is stable.
Background Information
- Current Earnings / Dividends
- Earnings per share in 1994 = $ 1.55
- Dividends per share in 1994 = $ 0.19
- Inputs for the High Growth Period
- Length of the High Growth Period = 5 years
- Expected growth rate = 36.00% (Based upon analyst projections)
- Beta during High Growth Period = 1.60
- Cost of Equity during High Growth Period = 7.5% + 1.60 (5.5%)
= 16.30%
- Dividend Payout Ratio = 12.03% (based on existing payout ratio)
- Inputs for the transition period
- Length of the transition period = 5 years
- Growth rate in earnings will decline from 36% in year 5 to 6%
in year 10 in linear increments.
- Payout ratio will increase from 12.03% to 60% over the same period
in linear increments.
- Beta will drop from 1.60 to 1.00 over the same period in linear
increments.
- Inputs for the Stable Growth
- Expected Growth Rate = 6%
- Beta during stable growth phase = 1.00 : Cost of Equity = 7.50%
+ 1.0 (5.5%) = 13.00%
- Payout Ratio = 60%
Estimating the Value
- These inputs are used to estimated expected earnings per share,
dividends per share and costs of equity for both the high growth
and stable periods. The present values are also shown.
|
Period
|
EPS
|
Payout Ratio
|
DPS
|
Cost of Equity
|
Present Value
|
|
1
|
$1.81
|
12.03%
|
$0.22
|
16.30%
|
$0.19
|
|
2
|
$2.46
|
12.03%
|
$0.30
|
16.30%
|
$0.22
|
|
3
|
$3.35
|
12.03%
|
$0.40
|
16.30%
|
$0.25
|
|
4
|
$4.55
|
12.03%
|
$0.55
|
16.30%
|
$0.30
|
|
5
|
$6.19
|
12.03%
|
$0.74
|
16.30%
|
$0.35
|
|
6
|
$8.04
|
21.62%
|
$1.74
|
15.64%
|
$0.71
|
|
7
|
$9.97
|
31.22%
|
$3.11
|
14.98%
|
$1.10
|
|
|
|
|
|
|