The Adjusted Present Value Approach

In the adjusted present value (APV) approach, we begin with the value of the firm without debt. As we add debt to the firm, we consider the net effect on value by considering both the benefits and the costs of borrowing. To do this, we assume that the primary benefit of borrowing is a tax benefit and that the most significant cost of borrowing is the added risk of bankruptcy.

The Mechanics of APV Valuation

We estimate the value of the firm in three steps. We begin by estimating the value of the firm with no leverage. We then consider the present value of the interest tax savings generated by borrowing a given amount of money. Finally, we evaluate the effect of borrowing the amount on the probability that the firm will go bankrupt, and the expected cost of bankruptcy.

Value of Unlevered Firm

The first step in this approach is the estimation of the value of the unlevered firm. This can be accomplished by valuing the firm as if it had no debt, i.e., by discounting the expected free cash flow to the firm at the unlevered cost of equity. In the special case where cash flows grow at a constant rate in perpetuity, the value of the firm is easily computed.

Value of Unlevered Firm =

where FCFF₀ is the current after-tax operating cash flow to the firm, r_u is the unlevered cost of equity and g is the expected growth rate. In the more general case, you can value the firm using any set of growth assumptions you believe are reasonable for the firm.

The inputs needed for this valuation are the expected cashflows, growth rates and the unlevered cost of equity. To estimate the latter, we can draw on our earlier analysis and compute the unlevered beta of the firm.

where

bunlevered = Unlevered beta of the firm

bcurrent = Current equity beta of the firm

t = Tax rate for the firm

D/E = Current debt/equity ratio

This unlevered beta can then be used to arrive at the unlevered cost of equity.

Expected Tax Benefit from Borrowing

The second step in this approach is the calculation of the expected tax benefit from a given level of debt. This tax benefit is a function of the tax rate of the firm and is discounted at the cost of debt to reflect the riskiness of this cash flow. If the tax savings are viewed as a perpetuity,

Value of Tax Benefits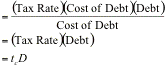

The tax rate used here is the firm’s marginal tax rate and it is assumed to stay constant over time. If we anticipate the tax rate changing over time, we can still compute the present value of tax benefits over time, but we cannot use the perpetual growth equation cited above.

Estimating Expected Bankruptcy Costs and Net Effect

The third step is to evaluate the effect of the given level of debt on the default risk of the firm and on expected bankruptcy costs. In theory, at least, this requires the estimation of the probability of default with the additional debt and the direct and indirect cost of bankruptcy. If p_a is the probability of default after the additional debt and BC is the present value of the bankruptcy cost, the present value of expected bankruptcy cost can be estimated.

PV of Expected Bankruptcy cost

This step of the adjusted present value approach poses the most significant estimation problem, since neither the probability of bankruptcy nor the bankruptcy cost can be estimated directly.

There are two basic ways in which the probability of bankruptcy can be estimated indirectly. One is to estimate a bond rating, as we did in the cost of capital approach, at each level of debt and use the empirical estimates of default probabilities for each rating. For instance, Table 15.8, extracted from a study by Altman and Kishore, summarizes the probability of default over ten years by bond rating class in 1998.[1]

Table 15.8: Default Rates by Bond Rating Classes

Bond Rating	Default Rate
D	100.00%
C	80.00%
CC	65.00%
CCC	46.61%
B-	32.50%
B	26.36%
B+	19.28%
BB	12.20%
BBB	2.30%
A-	1.41%
A	0.53%
A+	0.40%
AA	0.28%
AAA	0.01%

Source: Altman and Kishore (1998)

The other is to use a statistical approach, such as a probit to estimate the probability of default, based upon the firm’s observable characteristics, at each level of debt.

The bankruptcy cost can be estimated, albeit with considerable error, from studies that have looked at the magnitude of this cost in actual bankruptcies. Research that has looked at the direct cost of bankruptcy concludes that they are small[2], relative to firm value. The indirect costs of bankruptcy can be substantial, but the costs vary widely across firms. Shapiro and Titman speculate that the indirect costs could be as large as 25% to 30% of firm value but provide no direct evidence of the costs.

Illustration 15.5: Valuing a firm with the APV approach: Tube Investments

In Illustration 15.1, we valued Tube Investments, using a cost of capital approach. Here, we re-estimate the value of the firm using an adjusted present value approach in three steps.

Step 1: Unlevered firm value

To estimate the unlevered firm value, we first compute the unlevered beta. Tube Investment’s beta is 1.17, its current market debt to equity ratio is 79% and the firm’s tax rate is 30%.

Unlevered beta =

Using the rupee riskfree rate of 10.5% and the risk premium of 9.23% for India, we estimate an unlevered cost of equity.

Unlevered cost of equity = 10.5% + 0.75(9.23%) = 17.45%

Using the free cash flow to the firm that we estimated in Illustration 15.1 of Rs 212.2 million and the stable growth rate of 5%, we estimate the unlevered firm value:

Unlevered firm value=

Step 2: Tax benefits from debt

The tax benefits from debt are computed based upon Tube Investment’s existing dollar debt of Rs. 1807.3 million and the tax rate of 30%:

Expected tax benefits in perpetuity = Tax rate (Debt) = 0.30 (1807.3) = Rs 542.2 million

Step 3: Expected bankruptcy costs

To estimate this, we made two assumptions. First, based upon its existing rating, the probability of default at the existing debt level is 10%. Second,the cost of bankruptcy is 40% of unlevered firm value.

Expected bankruptcy cost =Probability of bankruptcy * Cost of bankruptcy * Unlevered firm value = 0.10*0.40*1704.6 = Rs 68.2 million

The value of the operating assets of the firm can now be estimated.

Value of the operating assets

= Unlevered firm value + PV of tax benefits – Expected Bankruptcy Costs

= 1704.6 + 542.2 – 68.2 = Rs 2178.6 million

Adding to this the value of cash and marketable securities of Rs. 1365.3 million, we obtain a value for the firm of Rs 3543.9 million. In contrast, we valued the firm at Rs. 3367.3 million with the cost of capital approach.

Cost of Capital versus APV Valuation

In an APV valuation, the value of a levered firm is obtained by adding the net effect of debt to the unlevered firm value.

Value of Levered Firm =

In the cost of capital approach, the effects of leverage show up in the cost of capital, with the tax benefit incorporated in the after-tax cost of debt and the bankruptcy costs in both the levered beta and the pre-tax cost of debt. Will the two approaches yield the same value? Not necessarily. The first reason for the differences is that the models consider bankruptcy costs very differently, with the adjusted present value approach providing more flexibility in allowing you to consider indirect bankruptcy costs. To the extent that these costs do not show up or show up inadequately in the pre-tax cost of debt, the APV approach will yield a more conservative estimate of value. The second reason is that the APV approach considers the tax benefit from a dollar debt value, usually based upon existing debt. The cost of capital approach estimates the tax benefit from a debt ratio that may require the firm to borrow increasing amounts in the future. For instance, assuming a market debt to capital ratio of 30% in perpetuity for a growing firm will require it to borrow more in the future and the tax benefit from expected future borrowings is incorporated into value today.

There are many who believe that adjusted present value is a more flexible way of approaching valuation than traditional discounted cash flow models. This may be true in a generic sense, but APV valuation in practice has significant flaws. The first and most important is that most practitioners who use the adjusted present value model ignore expected bankruptcy costs. Adding the tax benefits to unlevered firm value to get to the levered firm value makes debt seem like an unmixed blessing. Firm value will be overstated, especially at very high debt ratios, where the cost of bankruptcy is clearly not zero and, in some instances, the cost of bankruptcy is higher than the tax benefit of debt.

---

[1] This study estimated default rates over ten years only for some of the ratings classes. We extrapolated the rest of the ratings.

[2] In Warner’s study of railroad bankruptcies, the direct cost of bankruptcy seems to be about 5%.