SOLUTIONS

A GUIDE TO USING THE SOLUTIONS

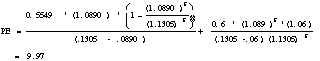
The following illustration is designed to explain the notation used in the solution manual.

Used in solutions

Should be read as

Revenues

Revenues

- Operating Expenses

(minus) Operating Expenses

- Depreciation

(minus) Depreciation

= EBIT

(results in) EBIT

- Interest Expenses

(minus) Interest Expenses

- Taxes

(minus) Taxes

= Net Income

(results in) Net Income

CHAPTER 1 - SOLUTIONS

INTRODUCTION TO VALUATION

Question 1

e. All of the above

Question 2

d. Value is determined by investor perceptions, but it is also determined by the underlying earnings and cash flows. Perceptions must be based upon reality.

Question 3

e. Either a,b, or c.

CHAPTER 2 - SOLUTIONS

APPROACHES TO VALUATION

Question 1

A. False. The reverse is generally true.

B. True. The value of an asset is an increasing function of its cash flows.

C. True. The value of an asset is an increasing function of its life.

D. False. Generally, the greater the uncertainty, the lower is the value of an asset.

E. False. The present value effect will translate the value of an asset from infinite to finite terms.

Question 2

A. It might be difficult to estimate how much of the success of the private firm is due to the owner's special skills and contacts.

B. Since the firm has no history of earnings and cash flow growth and, in fact, no potential for either in the near future, estimating near term cash flows may be impossible.

C. The firm's current earnings and cash flows may be depressed due to the recession. Other measures, such as debt-equity ratios and return on assets may also be affected.

D. Since discounted cash flow valuation requires positive cash flows some time in the near term, valuing troubled firms, which are likely to have negative cash flows in the foreseeable future, is likely to be difficult.

E. Restructuring alters the asset and liability mix of the firm, making it difficult to use historical data on earnings growth and cash flows on the firm.

F. Unutilized assets do not produce cash flows and hence do not show up in discounted cash flow valuation, unless they are considered separately.

Question 3

a. Value of Equity = $ 3,224

b. Value of Firm = $ 5,149

Question 4

A. Average P/E Ratio = 31.98

B. No. Eliminate the outliers, because they are likely to skew the average. The average P/E ratio without GET and King World is 25.16.

C. You are assuming that

(1) Paramount is similar to the average firm in the industry in terms of growth and risk.

(2) The marker is valuing communications firms correctly, on average.

CHAPTER 3 - SOLUTIONS

RISK AND RETURN

1.

a. False

b. True

c. False

d. False

e. False

f. False

g. False

h. False

2.

A. I would choose the stock market; higher returns and lower standard deviation

B. I would calculate the probability of these high payoffs (skewness) and build it into my decision process.

C. Expected Return = 8% (.5) + 20% (.5) = 14%

Standard Deviation = 12.93%

D. It will make gold prices have a positive correlation with stock prices, reducing the benefit from diversification.

3. You have just learnt about the Markowitz frontier and are eager to put it into practice.

a.

- Defining universe: Define assets that you will be picking your portfolio from (eg. S& P 500 stocks)

- Data requirements: Means and variances of each of the assets, as well as the covariances between each pair.

- Calculations and Statistics: For any given level of risk, find the portfolio that maximizes expected returns (across assets in the universe)

b. I would develop a matric that translated investor risk preferences into ìstandard deviationî constraints, and find the efficient portfolio that went with this standard deviation. I am assuming that standard deviation is the only measure of risk, and that the universe of assets from which I am creating this portfolio is a comprehensive one.

c.

- A massive disaster wiped out a hundred firms that used to be part of your universe: Move the frontiier in, i.e., reduce expected returns for each risk level

- You ignored foreign stocks initially, but now added them on: Move the frontier out

- A breakthrough in technology occurs, which cuts in half the cost of making computer chips: Move the frontier out.

4. Variance of a portfolio with n assets = (1/n) Average Variance + (n-1)/n Average Covariance

With 5 securities: (1/5) (50) + (4/5) (10) = 18%

With 10 securities: (1/10) (50) + (9/10) (10) = 14%

With 20 securities: (1/20) (50) + (19/20) (10) = 12%

With 50 securties: (1/50) (50) + (49/50) (10) = 10.8%

With 100 securities; (1/100) (50) + (99/100) (10) = 10.4%

Since the minimum variance is 10%, the portfolio has to contain about 50 securities before the variance is only 11%. (10% above the minimum)

5. The CAPM has been criticised on three grounds:

a. It makes unrealistic assumptions about transactions costs (there are none), private information (assumed to not exist), taxes and trading (all assets are divisible and traded). This critique is true but could probably be mounted against any risk and return model that aims to come up with practical models.

b. The parameters, which are estimated from historical data, are often noisy. This is true, but it is probably the weakest of the critiques. Estimation error is endemic in almost everything we do in finance.

3. It does not work very well. The Fama/French study noted that betas do not explain a significant proportion of the differences in returns across investments. It does not even explain as much as size and price/book value ratios. This is a potent criticism but could be countered by pointing out that from a predictive standpoint, the CAPM does as well as some of the suggested alternatives.,

6.

a. Both models assume that only market risk gets rewarded and measure this risk using betas.

b. The CAPM assumes that the market portfolio captures all of the market risk, whereas the APM allows for multiple sources of market risk and therefore multiple betas.

CHAPTER 4 - SOLUTIONS

ESTIMATION OF DISCOUNT RATES

Problem 1

a. Expected Return = 3% + 1.2 (8.5%) = 13.20%

b. Expected Price Appreciation = 13.20% - ($ 2.50 / $ 50) = 8.20%

Expected Price one year from today = $ 50 (1.082) = $ 54.10

c. Expected Returns over last year = 5% + 1.20 (-5% - 5%) = -7.00%

Returns on Market = -8% + 3% = -5%

d. Actual Returns over last year = (50-54+2)/54 = -3.70%

e. Unlevered Beta = 1.20 / (1+ (1-.4) (50/100)) = 0.923

If the firm issues $ 50 million in equity and retires debt, its beta will drop to 0.923

 

Problem 2

Unlevered Beta = 1.20 / (1 + (1-0.4) (50/100)) = 0.923076923

New Beta = 0.923 (1 + (1-0.4) (8)) =5.35

 

Problem 3

a. Unlevered Beta for Novell = 1.50 ! Firm has no debt

Unlevered Beta for WordPerfect = 1.30 ! Firm has no debt

Unlevered Beta for Combined Firm = 1.50 (2/(2+1)) + 1.30 (1/(2+1)) = 1.43

This would be the beta of the combined firm if the deal is all-equity.

b. If the deal is financed with debt,

New Debt/Equity Ratio = 1/2 = 0.5

New Beta = 1.43 (1 + (1-.4) (0.5)) = 1.86

 

Problem 4

a. Beta for Hewlett Packard = 1.10 (2/8) + 1.50 (2/8) + 2.00 (1/8) + 1.00 (3/8) = 1.275

This beta may not be equal to the regression estimate of beta, because both of these are estimated with error

b. Cost of Equity = 7.5% + 1.275 (5.5%) = 14.51%

Mainframes Cost of Equity = 7.5% + 1.10 (5.5%) = 13.55%

Personal Computers Cost of Equity = 7.5% + 1.5(5.5%) = 15.75%

Software Cost of Equity = 7.5% + 2 (5.5%) = 18.50%

Printer Division's Cost of Equity = 7.5% + 1 (5.5%) = 13.00%

To value the printer division, I would use a 13.00% cost of equity.

c. Assuming that the leverage is equally distributed across the divisions,

Division

Beta

Unlevered Beta

Value of Equity

Ascribed Debt

Firm Value

Mainframes

1.10

1.019

2.00

0.25

2.25

PCs

1.50

1.389

2.00

0.25

2.25

Software

2.00

1.852

1.00

0.125

1.13

Printers

1.00

0.926

3.00

0.375

3.38

Unlevered Beta = 1.389 (2.25/6.75) + 1.852 (1.125/6.75) + 0.926 (3.375/6.75) = 1.235

New Debt/Equity Ratio = 1/7

New Levered Beta = 1.235 (1 + (1-.4) (1/7)) = 1.34

CHAPTER 5 - SOLUTIONS

UNDERSTANDING FINANCIAL STATEMENTS

1. Statement of Cash Flows

Net Earnings = 350

Reconciling Net Earnings to Net Operating Cash

+ Depreciation & Amortization = 200

- Increase in Receivables = -31

- Increase in Inventory = -11

+ Increase in Payables = + 48

Net Cash from Operations = 556

Cash Flows from Investing

Capital Expenditures = -426 (Increase in Fixed Assets + Deprecn)

Net Cash Use in Investment Activities = -426

Cash Flows from Financing

Increase in Debt = +32

Dividends Paid = -84

Stock Bought Back = -101

Net Cash from Financing = --153

Decrease in Cash Balance = -23

 

2.

a. Pretax ROA = EBIT/ (Debt + Equity) = 637/(1240+820) = 30.92%

Aftertax ROA = 30.92% (1 - 215/565) = 19.16%

b. Return on Equity = 350/1240 = 28.23%

c. Pretax Operating Margin = EBIT/Sales = 637/4900 = 13.00%

Aftertax Operating Margin = 13.00% (1-215/565) = 8.05%

d. Net profit Margin = 350/4900 = 7.14%

3. Operating Leverage = Change in EBIT/Change in Saes = 100/600

= 0.16667

4. a. Book Value Debt/Equity Ratio = 820/1240 = 66.13%

b. Market Value Debt./Equity Ratio = (820*.95)/(71*60) = 18.29%

c. Book Value Debt/Capital Ratio = 820/2060 = 39.81%

d. Market Value Debt/Capital Ratio = (820*.95)/(71*60+820*.95)

= 15.46%

5. a. Working Capital in 1993 = (439+599+443)-732 = 749

Working Capital in 1994 = (450+630+420) - 780 = 720

b. Current Ratio in 1994 = (450+630+420)/780 = 1.92

c. Total Asset Turnover Rato = Sales/Total Assets = 4900/2840 = 1.73

Fixed Asset Turnover Ratio = Sales/Fixed Assets = 4900/1340 = 3.66
Accounts Receivable Turnover Ratio = Sales/Accounts Rec

= 4900/630 = 7.78

Inventory Turnover = COGS/Inventory = 4063/450 = 9.03

d. Number of Days of Sales = 365/ Inventory Turnover = 40.43

CHAPTER 6 - SOLUTIONS

ESTIMATION OF CASH FLOWS

Question 1

C. It is the cash that equity investors can take out of the firm after financing investment needed to sustain future growth.

Question 2

A. False. Capital expenditures may be greater than depreciation.

B. False. The dividends can exceed the free cash flow to equity.

C. True. The FCFF is a pre-debt cash flow. It can be equal to, but it cannot be lower than the FCFE.

D. False. The free cash flow to equity is after capital expenditures.

Question 3

A. FCFE in 1992 = $41.10 + $12.50 - $15 - (175 - 180) = $43.60 million

FCFE in 1993 = $48 + $14 - $18 - (240 - 175) = - $21 million

B. Working Capital as Proportion of Revenues: 1992 = 175/544 = 32.17%

Change in Revenues in 1993 = 620 - 544 = 76

FCFE in 1993 = $48 + $14 - $18 - (175/544) * (620 - 544)

= $19.55 million

Question 4

A. FCFE1992 = $117.9 + $573.5 - $800 - ($92 - $34.8) + (2000-1750)

= $84.20 million

FCFE1993 = $130 + $580 - $850 - (-370 - 92) + (2200 - 2000)

= $522 million

B. FCFF1992 = $117.9 million + $170 (1 - (652/770)) + $573.5 - $800 - ($92 - $34.8)

= - $139.75 million

(The tax rate is extraordinarily high = 652/770; the taxable income is 770 million (940 - 170))

FCFF in 1993 = $130 million + $172 (1 - (670/800)) + $580 - $850 -

(-370 - 92) = $349.95 million

C. Debt Ratio = $2200 million/($2200 million + 77 * $29) = 49.63%

1994 projection (in millions)

Net Income = $137.80

- (1 - 0.4963) * (850 - 580) * 1.06 = $144.16

FCFE = -$6.36

D. (Also in millions)

Net Income =

$137.80

- (1 - 0.75) * (850 - 580) * 1.06 =

$71.55

FCFE =

$66.25

Question 5

Year

FCFE/share

Terminal Value

Real CF

1

$1.12

$1.09

2

$1.25

$1.18

3

$1.40

$1.29

4

$1.57

$1.40

5

$1.76

$23.32

$21.63

Real Cash Flow = Nominal Cash Flowt/(1.03)t

A. Present Value = 1.12/1.14 + 1.25/1.142 + 1.40/1.143 + 1.57/1.144 + (1.76 + 23.32)/1.145 = $16.84

B. Real Discount Rate = 1.14/1.03 - 1 = 10.68%

Present Value =1.09/1.1068 + 1.18/1.10682 + 1.29/1.10683 + 1.40/1.10684 + (21.63)/1.10685 = $16.84

(Use real discount rates on real cash flows.)

CHAPTER 7 - SOLUTIONS

ESTIMATION OF GROWTH RATES

Question 1

Year

Year: No

EPS

ln(EPS)

Growth Rate

1989

1

$ 1.28

0.25

1990

2

$ 1.42

0.35

10.94%

1991

3

$ 1.58

0.46

11.27%

1992

4

$ 1.78

0.58

12.66%

1993

5

$ 1.98

0.68

11.24%

1994

6

$ 2.30

0.83

16.16%

a. Arithmetic Average =12.45%

Geometric Average = (2.30/1.28)(1/5) -1 = 12.44%

b. EPS(t) = 1.025 + 0.199 (t)

Growth rate = 0.199/Average EPS =11.55%

c. ln(EPS(t)) = 0.12 + 0.1156 (t) ! Growth rate is 11.56%

 

Question 2

Year

Year: No

EPS

Growth Rate

1989

1

$ 0.77

1990

2

$ (0.26)

-133.77%

1991

3

$ (0.90)

246.15%

1992

4

$ (1.39)

54.44%

1993

5

$ (0.65)

-113.85%

1994

6

$ 0.10

750.00%

Geometric average growth rate = ($0.10/$0.77)^(.2) -1 =-33.52%

 

Question 3

Expected Growth Rate = Retention Ratio * ROE = .63*.20 = 12.60%

For every 1% increase in the ROE, the expected growth rate will increase by 0.63%

 

Question 4

a. Net Income = (1488 - 90) * 0.6 = $ 838.80

ROE = 838.8/1790 =46.86%

Expected Growth Rate = 0.7 (46.86%) = 32.80%

b. Return on Assets = 1488 (1-0.4)/(1330+1790) = 28.62%

Interest Rate on Debt = 90/1330 = 6.77%

Book Value Debt/Equity Ratio = 1330/1790 = 74.30%

If debt ratio is doubled,

Net Interest Rate = 6.77% + 1% = 7.77%

Book Value D/E Ratio = 0.743 * 2 = 1.486

Expected ROE = 28.62% + 1.486 (28.62% - 7.77%) = 59.60%

Expected growth rate = 0.7 * 59.60% = 41.72%

c. Yes. I would expect the ROA to drop to industry averages.

 

Question 5

a. EBIT = .10 * 34500 = 3450

Assets = 34500/3 = 11500

ROA = 3450*0.64/11500 = 19.20%

b. If the margin drops to 8%,

ROA = 19.20% * (8/10) = 15.36%

CHAPTER 8 - SOLUTIONS

MARKET EFFICIENCY : DEFINITIONS AND TESTS

1. (a) Resources are allocated among firms efficiently (i.e. put to best use)

(f) No group of investors will do better than the market consistently after adjusting for risk and transactions costs.

2. No. The stock price should reflect this seasonal pattern in sales. If seasonal sales were better or worse than expected, you would expect to see an effect on stock prices.

3. To test any market inefficiency, a model needs to be specified for expected returns. One cannot therefore test market efficiency alone without jointly testing an asset pricing model

4. No. Demand and Supply are determined by real variables (including the intrinsic value).

5. You should have looked at the merger announcement date (in the WSJ) and not at the effective date. Furthermore you should have started looking at days before the announcement date. Finally, by focusing on only the twenty largest mergers, you may be inducing sampling bias into your conclusions.

6. (d) market prices contain errors, but the errors are random and therefore cannot be exploited by investors.

7.a. Decrease Efficiency

Reasoning: Increases transactions cost and allows inefficiencies to continue.

b. Decrease Efficiency

Reasoning: Removes an avenue that those with bad news could have used.

c. Increase Efficiency

Reasoning: Allows investors to trade on news more easily

d. Increase Efficiency

Reasoning: Allows more investors to come in and exploit inefficiencies.

8. (a) There is some insider trading going on,, or at least information leaking out.

(b) Suggests that the announcement contains good news, and that some of the news at least is a positive surprise to markets.

(c) Suggests that markets over reacted to the initial news and there is a price correction.

CHAPTER 9 - SOLUTIONS

MARKET EFFICIENCY ñ THE EVIDENCE

1. Small firms make a substantial premium over expected returns after adjusting for risk. Most of this premium is earned in the first fifteend days of the year. This may be because (a) we are measuring risk incorrectly (b) Transactions costs are higher (c) Information is much more scanty. If your transacitons costs are low enough, you could construct a portfolio of smaller stocks.

2. This suggests that markets do not react instantaneously to information events and that price adjustments to new informaition do not happen immediately. I would expect to find this to be much more of a problem with smaller, information-poor firms. I would exploit this anomaly by buying these stocks right after a positive surprise and selling after a negative surprise and holding for a very short time period. (The transactions costs and uncertainty might be much higher)

3. (a) Investors sell stocks on which they have made losses towards the end of the year (driving the price down) and buy them back after the turn of the year (causing prices go up)

(b) More information may come out in January than any other month of the year. Investors may be more optimistic and have more cash in January.

4.

9% (1-.4) + 5% (1-x) = 12% (1-.4) + 1% (1-x)

Solve for x, x = 55%

5. a. False. Low PE stocks are not riskier.

b. False. The small stock effect is not created by outliers.

c. False. Stock prices are affected but the average investor cannot take advantage of the price effect.

6. Expected Return on AD Value Fund = 6% + 0.8 (16%-6%) = 14%

Expected Return on AD Growth Fund = 6% + 1.2 (16%-6%) = 18%

AD Value outperformed the market by 2%

AD Growth underperformed by the market by 2%

b. (0.95) (1.02)^n = 1.00

Solve for n,

n = 2.59 years

CHAPTER 10 - SOLUTIONS

DIVIDEND DISCOUNT MODELS

Question 1

A. False. The dividend discount model can still be used to value the dividends that the company will pay after the high growth eases.

B. False. It depends upon the assumptions made about expected future growth and risk.

C. False. This will be true only if the stock market falls more than merited by changes in the fundamentals (such as growth and cash flows).

D. True. Portfolios of stocks that are undervalued using the dividend discount model seem to earn excess returns over long time periods.

E. True. The model is biased towards these stocks because of its emphasis on dividends.

Question 2

A. Cost of Equity = 6.25% + 0.90 * 5.5% = 11.20%

Value Per Share = $3.56 * 1.055/(.1120 - .055) = $65.89

B. $3.56 (1 + g)/(.1120 - g) = $80

Solving for g,

g = (80 * .112 - 3.56)/(80 + 3.56) = 6.46%

Question 3

A. Retention Ratio = 1 - Payout Ratio = 1 - 0.42/1.50 = 72%

Return on Assets

= (Net Income + Int Exp (1-t))/(BV of Debt + BV of Equity)

= (30 + 0.8 * (1 - 0.385))/(7.6 + 160) = 18.19%

Debt/Equity Ratio = 7.6/160 = .0475

Interest Rate on Debt = 0.8/7.6 = 10.53%

Expected Growth Rate

= 0.72 [.1819 + .0475 (.1819 - .1053 * (1 - 0.385))] = 13.5%

Alternatively, and much more simply,

Return on Equity = 30/160 = .1875

Expected Growth Rate = 0.72 * .1875 = 13.5%

B. Expected payout ratio after 1998:

= 1 - g/[ROA + D/E (ROA - i (1-t))]

= 1 - .06/(.125+.25(.125 - .07(1-.385))

= 0.5876

C. Beta in 1993 = 0.85

Unlevered Beta = 0.85/(1 + (1 - 0.385) * 0.05) = 0.8246

Beta After 1998 = 0.8246 * (1 + (1 - 0.385) * 0.25) = 0.95

D. Cost of Equity in 1999 = 7% + 0.95 * 5.5% = 12.23%

Expected Dividend in 1999

= ( $1.50 * 1.1355 * 1.06) * 0.5876 = $1.76

Expected Price at End of 1998 = $1.76/(.1223 - .06) = $28.25

E.

Year

EPS

DPS

1994

$1.70

$0.48

1995

$1.93

$0.54

1996

$2.19

$0.61

1997

$2.49

$0.70

1998

$2.83

$0.79

$28.25

Cost of Equity = 7% + 0.85 * 5.5% =

11.68%

PV of Dividends and Terminal Price (@ 11.68%) =

$18.47

F. Total Value per Share = $18.47

Value Per Share Using Gordon Growth Model

= $1.50 * 1.06 * 0.5876/(.1223 - .06) = $15.00

Value Per Share With No Growth = $1.50 * 0.5876/.1223 = $7.21

Value of Extraordinary Growth = $18.47 - $15.00 = $3.47

Value of Stable Growth = $15.00 - $7.21 = $7.79

Question 4

A. Cost of Equity = 6.25% + 0.85 * 5.5% = 10.93%

Value of Stable Growth = $0.48 * 1.07/(.1093 - .07) = $13.07

B. Value of Extraordinary Growth

= $0.48 * (6/2) * (.25 - .07)/(.1093 - .07) = $6.60

C. The payout ratio is assumed to remain unchanged as the growth rate changes. The payout ratio in this case is assumed to remain at 60% (0.48/0.80).

Question 5

A.

Period

EPS

DPS

1

$4.58

$0.79

2

$5.32

$0.92

3

$6.17

$1.07

4

$7.15

$1.21

5

$8.30

$1.43

6

$9.46

$2.35

7

$10.59

$3.56

8

$11.65

$4.94

9

$12.58

$6.44

10

$13.34

$8.00

B. Expected Price at End of 2003

= ($13.34 * 1.06 * 0.60)/(.1175 - .06) = $147.54

(Cost of Equity = 6.25% = 5.5% = 11.75%)

C.

PV of Dividends - High Growth =

$3.67

PV of Dividends - Transition =

$9.10

PV of Terminal Price =

$ 44.59

Value Per Share =

$57.36

CHAPTER 11 - SOLUTIONS

FREE CASH FLOW TO EQUITY DISCOUNT MODELS

Question 1

A. True. Dividends are generally smoothed out. Free cash flows to equity reflect the variability of the underlying earnings as well as the variability in capital expenditures.

B. False. Firms can have negative free cash flows to equity. Dividends cannot be less than zero.

C. False. Firms with high capital expenditures, relative to depreciation, may have lower FCFE than net income.

D. False. The free cash flow to equity can be negative for companies, which either have negative net income and/or high capital expenditures, relative to depreciation. This implies that new stock has to be issued.

Question 2

A. Value Per Share = $1.70 * 1.07/(.1203 - .07) = $36.20

(Cost of Equity = 6.25% + 1.05 * 5.50% = 12.03%)

B.

Current Earnings per share =

$3.20

- (1 - Desired Debt Fraction) *

(Capital Spending - Depreciation)

83.61%*

$1.00 =

$0.84

-(1 - Desired Debt Fraction) *

Chg Working Capital

= 83.61% * $0.00

$0.00

Free Cash Flow to Equity =

$2.36

Cost of Equity = 6.25% + 1.05 * 5.5% = 12.03%

Value Per Share = $2.36 * 1.07/(.1203 - .07) = $50.20

This is based upon the assumption that the current ratio of capital expenditures to depreciation is maintained in perpetuity.

C. The FCFE is greater than the dividends paid. The higher value from the model reflects the additional value from the cash accumulated in the firm. The FCFE value is more likely to reflect the true value.

Question 3

A.

Year

EPS

Cap Exp

Depr

D WC

FCFE

Term Price

1

$2.71

$2.60

$1.30

$0.05

$1.64

2

$3.13

$3.00

$1.50

$0.05

$1.89

3

$3.62

$3.47

$1.73

$0.05

$2.19

4

$4.18

$4.00

$2.00

$0.06

$2.54

5

$4.83

$4.62

$2.31

$0.06

$2.93

$84.74

6

$5.12

$4.90

$4.90

$0.04

$5.08

The net capital expenditures (Cap Ex - Depreciation) anChg Working Capital change is offset partially by debt (20%). The balance comes from equity. For instance, in year 1:

FCFE = $2.71 - ($2.60 - $1.30) * (1 - 0.20) - $0.05 * (1 - 0.20) = $1.64)

Cost of Equity = 6.5% + 1 * 5.5% = 12%

Terminal Value Per Share = $5.08/(.12 - .06) = $84.74

Present Value Per Share = 1.64/1.12 + 1.89/1.122 + 2.19/1.123 + 2.54/1.124 + (2.93 + 84.74)/1.125 = $55.89

B.

Year

EPS

Cap Exp

Depr

D WC

FCFE

Term Price

1

$2.71

$2.60

$1.30

$0.05

$1.64

2

$3.13

$3.00

$1.50

$0.05

$1.89

3

$3.62

$3.47

$1.73

$0.05

$2.19

4

$4.18

$4.00

$2.00

$0.06

$2.54

5

$4.83

$4.62

$2.31

$0.06

$2.93

$52.09

6

$5.12

$4.90

$2.45

$0.04

$3.13

Terminal Value Per Share = $3.13/(.12 - .06) = $52.09

Present Value Per Share = 1.64/1.12 + 1.89/1.122 + 2.19/1.123 + 2.54/1.124 + (2.93+52.09)/1.125 = $37.36

C.

Year

EPS

Cap Exp

Depr

D WC

FCFE

Term Price

1

$2.71

$2.60

$1.30

$0.05

$1.43

2

$3.13

$3.00

$1.50

$0.05

$1.66

3

$3.62

$3.47

$1.73

$0.05

$1.92

4

$4.18

$4.00

$2.00

$0.06

$2.23

5

$4.83

$4.62

$2.31

$0.06

$2.58

$45.85

6

$5.12

$4.90

$2.45

$0.04

$2.75

Terminal Value Per Share = $2.75/(.12 - .06) = $45.85

Present Value Per Share = 1.43/1.12 + 1.66/1.122 + 1.92/1.123 + 2.23/1.124 + (2.58 + 45.85)/1.125 = $32.87

The beta will probably be lower because of lower leverage.

Question 4

A.

Year

1

EPS

$2.30

Cap Ex

$0.68

Deprec

$0.33

D WC

$0.45

FCFE

$1.57

Term. Price

2

$2.63

$0.78

$0.37

$0.48

$1.82

3

$2.99

$0.89

$0.42

$0.51

$2.11

4

$3.41

$1.01

$0.48

$0.54

$2.45

5

$3.89

$1.16

$0.55

$0.57

$2.83

$52.69

6

$4.16

$0.88

$0.59

$0.20

$3.71

The net capital expenditures (Cap Ex - Depreciation) anChg Working Capital change is offset partially by debt (10%). The balance comes from equity. For instance, in year 1 -

FCFE = $2.30 - ($0.68 - $0.33) * (1 - 0.10) - $0.45 * (1 - 0.10) = $1.57)

B. Terminal Price = $3.71/ (.1305 - .07) = $52.69

C. Present Value Per Share = 1.57/1.136 + 1.82/1.1362 + 2.11/1.1363 + 2.45/1.1364 + (2.83 + 52.69)/1.1365 = $35.05

Question 5

A.

Year

1

2

3

4

5

Earnings

$0.66

$0.77

$0.90

$1.05

$1.23

(CapEx-Deprec'n) * (1-)

$0.05

$0.06

$0.07

$0.08

$0.10

Chg Working Capital * (1-)

$0.27

$0.31

$0.37

$0.43

$0.50

FCFE

$0.34

$0.39

$0.46

$0.54

$0.63

Present Value

$0.29

$0.30

$0.30

$0.31

$0.31

Transition Period (up to ten years)

Year

6

7

8

9

10

Growth Rate

14.60%

12.20%

9.80%

7.40%

5.00%

Cumulated Growth

14.60%

28.58%

41.18%

51.63%

59.21%

Earnings

$1.41

$1.58

$1.73

$1.86

$1.95

(CapEx-Deprec'n) * (1-)

$0.11

$0.13

$0.14

$0.15

$0.16

Chg Working Capital * (1-)

$0.45

$0.39

$0.30

$0.22

$0.13

FCFE

$0.84

$1.07

$1.29

$1.50

$1.67

Beta

1.38

1.31

1.24

1.17

1.10

Cost of Equity

14.59%

14.21%

13.82%

13.44%

13.05%

Present Value

$0.37

$0.41

$0.43

$0.44

$0.43

End-of-Life Index

1

Stable Growth Phase

Growth Rate: Stable Phase =

5.00%

FCFE in Terminal Year =

$1.92

Cost of Equity in Stable Phase =

13.05%

Price at the End of Growth Phase =

$23.79

PV of FCFE in High Growth Phase =

$ 1.51

Present Value of FCFE in Transition Phase =

$ 2.08

Present Value of Terminal Price =

$ 6.20

Value of the Stock =

$9.79

 

B.

Year

1

2

3

4

5

Earnings

$0.66

$0.77

$0.90

$1.05

$1.23

(CapEx-Deprec'n)* (1-)

$0.05

$0.06

$0.07

$0.08

$0.10

Chg Working Capital * (1-)

$0.27

$0.31

$0.37

$0.43

$0.50

FCFE

$0.34

$0.39

$0.46

$0.54

$0.63

Present Value

$0.29

$0.30

$0.30

$0.31

$0.31

Transition Period (up to ten years)

Year

6

7

8

9

10

Growth Rate

14.60%

12.20%

9.80%

7.40%

5.00%

Cumulated Growth

14.60%

28.58%

41.18%

51.63%

59.21%

Earnings

$1.41

$1.58

$1.73

$1.86

$1.95

(CapEx-Deprec'n)*(1-)

$0.11

$0.13

$0.14

$0.15

$0.16

Chg Working Capital *(1-)

$0.50

$0.48

$0.43

$0.36

$0.26

FCFE

$0.79

$0.97

$1.16

$1.35

$1.54

Beta

1.38

1.31

1.24

1.17

1.10

Cost of Equity

14.59%

14.21%

13.82%

13.44%

13.05%

Present Value

$0.34

$0.37

$0.39

$0.40

$0.40

End-of-Life Index

1

Stable Growth Phase

Growth Rate in Stable Phase =

5.00%

FCFE in Terminal Year =

$1.78

Cost of Equity in Stable Phase =

13.05%

Price at the End of Growth Phase =

$22.09

PV of FCFE in High Growth Phase =

$ 1.51

Present Value of FCFE in Transition Phase =

$ 1.90

Present Value of Terminal Price =

$ 5.76

Value of the Stock =

$ 9.17

C.

Year

1

2

3

4

5

Earnings

$0.66

$0.77

$0.90

$1.05

$1.23

(CapEx-Deprec'n) * (1-)

$0.05

$0.06

$0.07

$0.08

$0.10

D Working Capital * (1-)

$0.27

$0.31

$0.37

$0.43

$0.50

FCFE

$0.34

$0.39

$0.46

$0.54

$0.63

Present Value

$0.29

$0.30

$0.30

$0.31

$0.31

Transition Period (up to ten years)

Year

6

7

8

9

10

Growth Rate

14.60%

12.20%

9.80%

7.40%

5.00%

Cumulated Growth

14.60%

28.58%

41.18%

51.63%

59.21%

Earnings

$1.41

$1.58

$1.73

$1.86

$1.95

(CapEx-Deprec'n) * (1-)

$0.11

$0.13

$0.14

$0.15

$0.16

D Working Capital * (1-)

$0.45

$0.39

$0.30

$0.22

$0.13

FCFE

$0.84

$1.07

$1.29

$1.50

$1.67

Beta

1.45

1.45

1.45

1.45

1.45

Cost of Equity

14.98%

14.98%

14.98%

14.98%

14.98%

Present Value

$0.36

$0.40

$0.42

$0.43

$0.41

End-of-Life Index

1

Stable Growth Phase

Growth Rate in Stable Phase =

5.00%

FCFE in Terminal Year =

$1.92

Cost Of Equity in Stable Phase =

14.98%

Price at End of Growth Phase =

$19.19

PV of FCFE In High Growth Phase =

$1.51

Present Value of FCFE in Transition Phase =

$2.03

Present Value of Terminal Price =

$4.75

Value of the Stock =

$8.29

Question 6

A. Both models should have the same value, as long as a higher growth rate in earnings is used in the dividend discount model to reflect the growth created by the interest earned, and a lower beta to reflect the reduction in risk. The reality, however, is that most analysts will not make this adjustment, and the dividend discount model value will be lower than the FCFE model value.

B. The dividend discount model will overstate the true value, because it will not reflect the dilution that is inherent in the issue of new stock.

C. Both models should provide the same value.

D. Since acquisition, with the intent of diversifying, implies that the firm is paying too much (i.e., negative net present value), the dividend discount model will provide a lower value than the FCFE model.

E. If the firm is over-levered to begin with, and borrows more money, there will be a loss of value from the over-leverage. The FCFE model will reflect this lost value, and will thus provide a lower estimate of value than the dividend discount model.

CHAPTER 12 - SOLUTIONS

VALUING A FIRM - THE FCFF APPROACH

Question 1

A. False. It can be equal to the FCFE if the firm has no debt.

B. True.

C. False. It is pre-debt, but after-tax.

D. False. It is after-tax, but pre-debt.

E. False. The free cash flow to firm can be estimated directly from the earnings before interest and taxes.

Question 2

A. FCFF in 1993 = Net Income + Depreciation - Capital Expenditures - DWorking Capital + Interest Expenses (1 - tax rate)

= $770 + $960 - $1200 - 0 + $320 (1 - 0.36) = $734.80 million

B. EBIT = Net Income/(1 - tax rate) + Interest Expenses

= 770/0.64 + 320 = $1523.125 million

Return on Assets = EBIT (1-t)/ (BV of Debt + BV of Equity)

= 974.80/9000 = 10.83%

Expected Growth Rate in FCFF = Retention Ratio * ROA

= 0.6 * 10.83% = 6.50%

Cost of Equity = 7% + 1.05 * 5.5% = 12.775%

Cost of Capital = 8% (1 - 0.36) (4000/(4000 + 12000)) + 12.775% (12000/(4000 + 12000)) = 10.86%

Value of the Firm = 734.80/(.1086 - .065) = $16,853 millions

C. Value of Equity = Value of Firm - Market Value of Debt

= $16,853 - $4,000 = $12,853 millions

Value Per Share = $12,853/200 = $64.27

Question 3

A.

Yr

EBITDA

Deprec'n

EBIT

EBIT

Cap

ChgWC

FCFF

Term

(1-t)

Exp.

Value

0

$1,290

$400

$890

$534

$450

$82

$402

1

$1,413

$438

$975

$585

$493

$90

$440

2

$1,547

$480

$1,067

$640

$540

$98

$482

3

$1,694

$525

$1,169

$701

$591

$108

$528

4

$1,855

$575

$1,280

$768

$647

$118

$578

5

$2,031

$630

$1,401

$841

$708

$129

$633

$14,941

'93-97

After 1998

Cost of Equity =

13.05%

11.89%

AT Cost of Debt =

4.80%

4.50%

Cost of Capital =

9.37%

9.45%

Terminal Value

= {EBIT (1-t)(1+g) - (Rev1998 - Rev1997) * WC as % of Rev}/(WACC-g)

= (841 * 1.04) - (13500 * 1.0955 * 1.04 - 13500 * 1.0955)

* 0.07 /(.0945-.04) = $14,941

Value of the Firm

= 440/1.0937 + 482/1.09372 + 528/1.09373 + 578/1.09374 + (633 + 14941)/1.09375 = $11,566

B. Value of Equity in the Firm = ($11566 - Market Value of Debt) = 11566 - 3200 = 8366

Value Per Share = $8366/62 = $134.94

Question 4

A. Beta for the Health Division = 1.15

Cost of Equity = 7% + 1.15 * 5.5% = 13.33%

Cost of Capital = 13.33% * 0.80 + (7.5% * 0.6) * 0.2 = 11.56%

B.

Year

Deprec'n

EBIT

EBIT(1-t)

Cap Ex

FCFF

Term Val

0

$350

$560

$336

$420

$266

1

$364

$594

$356

$437

$283

2

$379

$629

$378

$454

$302

3

$394

$667

$400

$472

$321

4

$409

$707

$424

$491

$342

5

$426

$749

$450

$511

$364

$5,014

Now

After 5 years

Cost of Equity =

13.33%

13.33%

Cost of Debt =

4.50%

4.50%

Cost of Capital =

11.56%

11.56%

Value of the Division = 283/1.1156 + 302/1.11562 + 321/1.11563 + 342/1.11564 + (364 + 5014)/1.11565 = $4,062 millions

C. There might be potential for synergy, with an acquirer with related businesses. The health division at Kodak might also be mismanaged, creating the potential for additional value from better management.

Question 5

Value = FCFF /(WACC-g)

750 = 30/(WACC-.05)

Solving for WACC,

WACC = .09

Given the cost of equity of 12% and the after-tax cost of debt of 95,

Book Value weight for Equity = 0.50

The correct weights will be as follows:

Market Value Weight of Equity = (3*50)/(3*50+50) = 0.75

Correct Cost of Capital = 12% (.75) + 6% (.25) = 10.5%

Correct Value of Firm = 30/(.105-.05) = $545.45

Question 6

A. Cost of Equity = 7% + 1.25 * 5.5% = 13.88%

Current Debt Ratio = 1340/(1340 + 18.25 * 183.1) = 28.63%

After-tax Cost of Debt = 7.43% (1 - 0.4) = 4.46%

Cost of Capital = 13.88% (0.7137) + 4.46% (0.2863) = 11.18%

B. & C. See table below.

D/(D+E)

Cost of

Beta

Cost of

AT Cost of

Cost of

Firm

Debt

Equity

Debt

Capital

Value

0%

6.23%

1.01

12.54%

3.74%

12.54%

$2,604

10%

6.23%

1.07

12.91%

3.74%

11.99%

$2,763

20%

6.93%

1.16

13.37%

4.16%

11.53%

$2,912

30%

7.43%

1.27

13.97%

4.46%

11.11%

$3,063

40%

8.43%

1.41

14.76%

5.06%

10.88%

$3,153

50%

8.93%

1.61

15.87%

5.36%

10.61%

$3,265

60%

10.93%

1.91

17.53%

6.56%

10.95%

$3,125

70%

11.93%

2.42

20.30%

7.16%

11.10%

$3,067

80%

11.93%

3.43

25.84%

7.16%

10.89%

$3,149

90%

13.43%

6.45

42.47%

8.06%

11.50%

$2,923

Unlevered Beta = 1.25/(1 + 0.6 * (1340/(183.1 * 18.25)) = 1.01

Levered Beta at 10% D/(D+E) = 1.01 * (1 + 0.6 * (10/90)) = 1.07

FCFF to Firm Next Year = (637 - 235) * (1 - 0.4) * 1.03 = $248.43 million

Value of the Firm = 255.67 * 1.03/(WACC-.03)

CHAPTER 13 - SOLUTIONS

SPECIAL CASES IN VALUATION

Question 1

A.

Year

EPS

1984

$0.69

1985

$0.71

1986

$0.90

1987

$1.00

1988

$0.76

1989

$0.68

1990

$0.09

1991

$0.16

1992

($0.07)

1993

($0.15)

Average Earnings Per Share =

$0.48

Normalized Earnings Per Share in 1994 = $0.48 * 1.06 = $0.51

B.

Normalized Earnings Per Share =

$0.51

- (Cap Ex - Deprec'n) * (1 - Debt ratio) =

$0.25

- Chg Working Capital * (1- Debt ratio) =

$0.06

Normalized FCFE Next Year =

$0.19

(Assume that capital expenditures and depreciation will grow 6% in 1994.)

Question 2

A.

Total Assets in 1993 =

$25,000

(in millions)

Normalized Return on Assets =

12%

Normalized Return on Assets (pre-tax) =

20%

Normalized Income statement (based upon 12% ROA)

Earnings Before Interest and Taxes =

5000

Interest Expenses =

1400

Earnings Before Taxes =

3600

Taxes (at 40%) =

1440

Net Income =

2160

- (Cap Ex - Deprec'n) * (1-Debt ratio) =

500

FCFE

1660

Cost of Equity = 7% + 1.1 * 5.5% =

13.05%

Expected Growth Rate =

5%

Earnings before interest and taxes is calculated using the ROA:

ROA = EBIT (1- tax rate) / Total Assets = 12% (given in the problem)

Value of Equity = (1660 * 1.05)/(.1305 - .05) = $21,652

B. Value of Equity = $21,652/1.13052 = $16,942

Question 3

A.

Earnings Before Interest and Taxes =

$52.70

- Interest Expense =

$17.00

Earnings Before Taxes =

$35.70

- Taxes (40%)

$14.28

Earnings After Taxes =

$21.42

- (Cap Ex - Deprec'n) * (1-Debt Ratio) =

$3.75

- Chg Working Capital * (1- Debt Ratio) =

$4.76

FCFE =

$12.91

EBIT = Interest Expense * Interest Coverage Rate = $17 * 3.10 = $ 52.70

The change in working capital is based upon revenues growing at 4%.

B. Cost of Equity = 7% + 1.1 * 5.5% = 13.05%

Expected Growth Rate = 4%

Value of Equity = 12.91 * 1.04/(.1305 - .04) = $148.36 million

Question 4

A.

Year

Net Income

(in millions)

1987

$0.30

1988

$11.50

1989

($2.40)

1990

$7.20

1991

($4.60)

1992

($1.90)

Average =

$1.68

Net Income =

$1.68

- (Cap Ex - Deprec'n) * (1 - Debt ratio) =

1.30

= FCFE =

$0.38

B. Cost of Equity (until 1996) = 7% +1.2 * 5.5% = 13.6%

Cost of Equity (after 1996) = 7% + 5.5% = 12.5%

Year

Net Income

(Cap. Ex - Deprec'n) *

FCFE

Terminal Value

(1 - Debt Ratio)

1993

$1.78

$1.37

$0.42

1994

$1.89

$1.43

$0.45

1995

$2.00

$1.50

$0.50

1996

$2.12

$1.58

$0.54

$29.73

Term Year

$2.23

$0.00

$2.23

Capital expenditures are offset by depreciation in the terminal year.

Terminal Value = $2.23/(.125 - .05) = $29.73

Value of Equity

= 0.42/1.136 + 0.45/1.1362 + 0.50/1.1363 + (0.54 + 29.73)/1.1364

= $19.24 million

Value per Share = $ 19.24 million/ Number of Shares outstanding

Question 5

A.

Equity

Debt

Market Value Weight

61.61%

38.39%

Cost of Component

13.33%

5.10%

Cost of Capital = 13.33% (0.6161) + 5.1% (0.3839) = 10.17%

B.

Year

1993

1994

1995

1996

Terminal Year

EBIT (1-t)

$8.25

$9.08

$9.98

$10.98

$11.42

- (Cap Ex - Deprec'n)

$0.00

$0.00

$0.00

$0.00

$0.00

- Chg Working Capital

$0.00

$0.00

$0.00

$0.00

$0.00

= FCFF

$8.25

$9.08

$9.98

$10.98

$11.42

Terminal Value

$185.18

Terminal Value = $11.42/(.1017 - .04) = $185.18

Present Value = $8.25/1.1017 + $9.08/1.10172 + $9.98/1.10173 + ($10.98 + $185.18)/1.10174 = $155.60 million

C. Value of Equity = Value of Firm - Market Value of Debt = $155.60 - $109 = $46.60 million

Value of Equity Per Share = $46.60/15.9 = $2.93

Question 6

A. Unlevered Beta for Publicly Traded Firms in Same Business

= 1.30/(1 + 0.6 * 0.2) = 1.16

Debt/Equity Ratio for Private Firm

= Debt/Estimated Market Value of Equity = 10/30 = 33.33%

New Levered Beta For Private Firm = 1.16 * (1 + 0.6 * .3333) = 1.39

New Cost Of Equity = 7% + 1.39 * 5.5% = 14.66%

B. Pre-Tax Cost of Debt = $1/$10 = 10%

After-Tax Cost of Debt = 10% (1 - 0.4) = 6%

Cost of Capital = 6% (0.25) + 14.66% (0.75) = 12.49%

C. Using the Firm Approach:

1

2

3

4

5

Terminal

year

EBIT

$2.40

$2.88

$3.46

$4.15

$4.98

$5.23

EBIT (1 - tax rate)

$1.44

$1.73

$2.07

$2.49

$2.99

$3.14

- (Cap Ex - Deprec'n)

$0.60

$0.72

$0.86

$1.04

$1.24

$0.00

= FCFF

$0.84

$1.01

$1.21

$1.45

$1.74

$3.14

Terminal Value

$41.85

Terminal Value = $3.14/(.1249 - .05) = $41.85

Present Value (Value of Firm) (@ 12.49%) = $0.84/1.1249 + $1.01/1.12492 + $1.21/1.12493 + $1.45/1.12494 + ($1.74 + $41.85)/1.12495 = $27.50 million

Value of Equity = $27.50 million - $10 million = $17.50 million

Using the Equity approach:

1

2

3

4

5

Terminal

year

Net Income

$0.75

$0.94

$1.17

$1.46

$1.83

$1.98

- (Cap Ex - Deprec'n) * (1- Debt ratio) =

 

$0.45

 

$0.54

 

$0.65

 

$0.78

 

$0.93

 

$0.00

= FCFE

$0.30

$0.40

$0.52

$0.69

$0.90

$1.98

Terminal Value of Equity

$29.71

Terminal Value of Equity = $1.98/(.1466 - .05) = $29.71

Present Value (using Cost of Equity of 14.66%) = $0.30/1.1466 + $0.40/1.14662 + $0.52/1.14663 + $0.69/1.14664 + ($0.90 + $29.71)/1.14665 = $16.76 million

CHAPTER 14 - SOLUTIONS

PRICE/EARNINGS RATIOS

Question 1

A. Payout Ratio = 1.06/$2.40 = 44.17 %

Expected Growth Rate = 6%

Cost of Equity = 7% + 1.05 * 5.5% = 12.775%

P/E Ratio = 0.4417 * 1.06/(.12775 - .06) = 6.91

B. The stock is trading at ten times earnings.

P/E Ratio = 10 = 0.4417 (1+g)/(.12775-g)

Solving for g in this equation,

g = (1.2775 - 0.4417)/10.4417 = 8.00%

Question 2

A. Dividend Payout Ratio = Dividend Yield/(1/P/E)

= 0.025/(1/16.9) = 0.4225

Expected Growth Rate

= (1+Real Growth Rate) (1+ Expected Inflation) - 1

= 1.035 * 1.025 -1 = 6.09%

Cost of Equity = 6.95% + 5.5% = 12.45%

Expected P/E Ratio = Payout * (1 + g)/(r - g)

= 0.4225 * 1.0609/(.1245 - .0609) = 7.05

B. P/E Ratio = 16.9 = 0.4225 (1+g)/(.1245 - g)

Solving for g,

g = (16.9 * .1245 - 0.4225)/(16.9 + 0.4225) = 9.71%

C. Yes. It has to be real growth. If the growth arises because of higher inflation, interest rates will also rise, erasing much of the benefits of higher growth.

Question 3

A.

First 5 Years

After Year 5

Dividend Payout Ratio =

55.49%

60.00%

Return On Equity =

20.00%

15.00%

Expected Growth Rate =

8.90%

6.00%

Cost Of Equity =

13.05%

13.05%

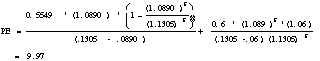
B. P/E Ratio Based Upon Stable Growth (6%; 60% dividend payout)

= 0.6 * 1.06/(.1305 - .06) = 9.02

Difference Due to High Growth = 9.97 - 9.02 = 0.95

Question 4

A.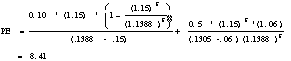

B. Growth Rate from 1983 to 1993 = (0.78/0.08)(1/10) -1 = 25.57%

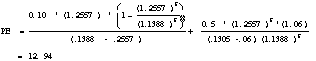
C.

Question 5

A. Dividend Payout Ratio = 0.0274/(1/21.2) = 0.581

Cost of Equity = 6% + 5.5% = 11.5%

Solving for the Implied Growth Rate

g = (21.2 * .115 - 0.581)/(21.2 + .581) = 8.53%

1+g = (1+ Expected Inflation Rate) (1+ Real Growth Rate)

Solving for Expected Inflation

1.0853 = (1+Expected Inflation rate) (1.025)

Expected Inflation Rate = 1.0853/1.025 - 1 = 5.88%

B. The P/E ratio would go down. For instance, in the formulation above,

Dividend Payout Ratio = 0.581

Cost of Equity = 12.5%

Expected Growth Rate =8.53%

The new P/E ratio would be

P/E = 0.581 (1.0853)/(.125 - .0853) = 15.88

C. Not necessarily. If the increase in expected real growth is greater than the increase in interest rates, P/E ratios may go up as interest rates go up.

Question 6

A. Average P/E Ratio for the Industry = 13.2

Median P/E Ratio for the Industry = 12.25

If the firms in this group are homogeneous, the average P/E ratio provides an estimate of how much the market values earnings in this sector, given the expected growth potential and the risk in the sector.

The average P/E ratio can be skewed by extreme values (usually high, since P/E cannot be less than zero). The median corrects for this by looking at the median firm in the sector.

B. This statement is likely to be true only if

(1) Thiokol has the same growth prospects and risk profile of the typical firm in the industry. It also generates cash flows for disbursement as dividends which are similar to the typical firm in the industry.

(2) Thiokol has higher growth potential and/or lower risk than the typical firm in the industry.

C. The regression of P/E ratios on fundamentals yields the following:

P/E = -2.33 + 35.74 Growth Rate + 11.97 Beta + 2.90 Payout Ratio

R2= 0.4068

The following table provides predicted P/E ratios for the firms in the group:

Actual P/E

Predicted P/E

Difference

Boeing

17.30

12.90

4.40

General Dynamics

15.50

17.90

-2.40

GM- Hughes

16.50

13.68

2.82

Grumman

11.40

12.07

-0.67

Lockheed Corp.

10.20

12.31

-2.11

Logicon

12.40

13.17

-0.77

Loral Corporation

13.30

13.21

0.09

Martin Marietta

11.00

11.34

-0.34

McDonnell Doug.

22.60

17.15

5.45

Northrop

9.50

14.82

-5.32

Raytheon

12.10

10.85

1.25

Rockwell

13.90

14.85

-0.95

Thiokol

8.70

11.44

-2.74

United Industrial

10.40

9.11

1.29

Again, negative numbers indicate that the stock is undervalued.

The problem with a regression like this one is that it has relatively few observations and is likely to be thrown off by a few extreme observations.

Question 7

A. Expected Growth Rate = 25%

Unlevered Beta = 1.15/(1 + 0.6 * 0.25) = 1.00

FCFE = Net Income + Depreciation - Capital Spending = 10 + 5 - 12 = 3

Estimated Dividend Payout Ratio = 3/10 = 30%

P/E = 18.69 + 0.0695 * 25 - 0.5082 (1.00) - 0.4262 * 0.30 = 19.79

B.

1. The cross-sectional relationship between P/E ratio and the fundamentals may change over time.

2. The market might be overvaluing all stocks.

3. Some of the fundamentals, such as growth rate or beta, might be estimated with error.

CHAPTER 15 - SOLUTIONS

PRICE/BOOK VALUE MULTIPLES

Question 1

A. False. If the ROE< Required rate of return, this can be justified.

B. False, since the drop can be temporary. If the drop is permanent, this will be generally true, since there will be a two-layered impact. The growth will go down, pushing down Price/Book value ratios. The ROE will also go down pushing P/BV ratios down even further.

C. True.

D. True. If other things (like risk) are not equal, this can be false.

E. False. The growth rate will be lower for these firms. The net effect may be a lower price/book value ratio.

Question 2

A. Dividend Payout Ratio = $2/$4 = 50%

Return on Equity = $4/$40 = 10%

Cost of Equity = 7% +0.85 * 5.5% = 11.68%

Expected Growth Rate = 6%

Price/Book Value Ratio = (.1) (.5)(1.06)/(.1168 - .06) = 0.93

A simpler solution might be the following:

Price/Book Value Ratio = (.10 - .06)/(.1168 - .06) = 0.70

(This solution takes into account the relationship between ROE and g, i.e., g=b(ROE))

B. If the P/BV ratio is 1.5, using the first approach,

1.5 = ROE (.5) (1.06)/(.1168 - .06),

Solving for ROE = 16.08%

Using the second approach,

1.5 = (ROE - .06)/(.1168 - .06)

Solving for ROE = 14.52%

Question 3

A. Average Price/Book Value Ratio = 2.28

Average ROE = 12.44%

Average Beta = 1.10

B. Cost of Equity (based upon average beta) = 7% + 1.1 * 5.5%

= 13.05%

If P/BV = (ROE - g)/(r - g),

and ROE < r, (as in this case)

then P/BV <1.

Therefore, one may conclude that stocks in the industry are, on average, overvalued relative to book value (assuming that the industry overall is in stable growth, although individual firms might still have extraordinary growth).

Question 4

A.

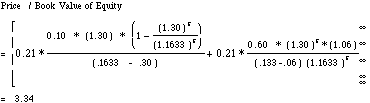
B.

Growth Rate

Price/Book Value Ratio

10%

1.47

15%

1.83

20%

2.25

25%

2.75

30%

3.34

40%

4.81

50%

6.76

C. Between 11 and 12 years (this can be solved through trial and error).

Question 5

A.

Next 10 yrs

After yr 10

Payout Ratio

37.00%

60.00%

Expected Growth

19.85%

6.00%

Cost of Equity

12.88%

11.50%

ROE

31.50%

15.00%

Expected Growth Rate = (1 - Payout Ratio)*ROE = (1 - .37) (.3150)

= .1985

Payout Ratio After Year 10 = 1 - Growth Rate / ROE

= 1 - 6%/15% = .60

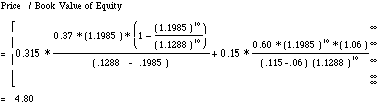
B.

Next 10 years

After year 10

Payout Ratio

37.00%

60.00%

Expected Growth

12.60%

6.00%

Cost of Equity

12.88%

11.50%

ROE

20.00%

15.00%

Expected Growth Rate = (1 - Payout Ratio)*ROE = (1 - .37) (.20)

= .126

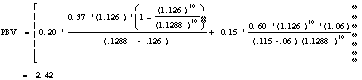
Question 6

A. The R squared of the regression measures the goodness of fit of the regression. A high R squared would provide the user with more comfort with the predictions from using the regression.

B. P/BV = 0.88 + 0.82 (0.2857) + 7.79 (.25) - 0.41 (1.05) + 13.81 (.175) = 5.05

This regression uses the information in the entire cross-section, and hence might capture more of the differences across firms in other industries.

CHAPTER 16 - SOLUTIONS

PRICE/SALES MULTIPLES

Question 1

A. Dividend Payout Ratio = $1.12/$2.45 = 0.4571

Expected Growth Rate = 6%

Cost of Equity = 7% + 0.9 (5.5%) = 11.95%

Profit Margin = 2.45/122 = 2%

P/S Ratio = .02 * 0.4571 * (1.06)/(.1195 - .06) = 0.16288

Price Based on this Multiple = 0.16288 * 122 = $19.87

B. P/S Ratio Needed for a Price of $34 = $34/122 = 0.2787

Profit Margin Needed for this P/S Ratio

= 0.2787 * (.1195 - .06)/(0.4571 * 1.06)

= 0.0342 or 3.42%

Question 2

A. These are the two companies with high expected growth rates. These high growth rates may explain the high P/S ratios. In addition, the Bombay company has the highest profit margin of the group.

B.

Correlation between P/S ratio and profit margin =

0.8840

Correlation between P/S ratio and expected growth =

0.7694

Correlation between P/S ratio and beta =

0.2754

Correlation between P/S ratio and payout =

-0.4390

C.

One measure that might work is the ratio of Price/Sales (P/S) ratio to profit margin. On this basis, Bradlee's which has a P/S ratio of 0.09 and a profit margin of 1.04%, Caldor and Sears are most likely to be undervalued, whereas the Bombay company with P/S-Margin ratio of 0.56 is most likely to be overvalued.

Company

Price

Sales

P/S

Profit

Exp.

Beta

P/S-

Ratio

Margin

Growth

Margin

Bombay Co.

$38

$9.70

3.92

7.01%

29.00%

1.45

0.559

Bradlees

15

168.6

0.09

1.04%

12.00%

1.15

0.086

Caldor

32

147.45

0.22

1.83%

12.50%

1.55

0.119

Consol. Store

21

23

0.91

4.13%

26.50%

1.35

0.221

Dayton Hudson

73

272.9

0.27

1.70%

12.50%

1.3

0.157

Federated

22

58.9

0.37

2.38%

10.00%

1.45

0.157

Kmart

23

101.45

0.23

1.72%

11.50%

1.3

0.131

Nordstrom

36

43.85

0.82

3.65%

11.50%

1.45

0.225

Penney

54

81.05

0.67

4.32%

10.50%

1.1

0.154

Sears

57

150

0.38

3.03%

11.00%

1.35

0.125

Tiffany's

32

35.65

0.9

4.21%

10.50%

1.5

0.213

Wal-Mart

30

29.35

1.02

3.58%

18.50%

1.3

0.286

Woolworth

23

74.15

0.31

1.82%

13.00%

1.25

0.17

Alternatively, a regression of P/S ratios against the fundamental variables could have been run and estimated P/S ratios can be obtained.

Question 3

A.

Profit Margin = 221/8298 = 2.66%

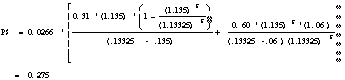
B. P/S ratio for Stable Growth Firm with Same Margin

= 0.0266 * 0.6 * 1.06/(.13325 - .06) = 0.231

P/S ratio attributable to High Growth = 0.275 - 0.231 = 0.044

Question 4

A.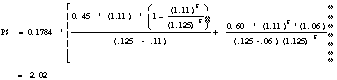

B. New Margin = 100/700 = 14.29%

Old Growth Rate

= Old Profit Margin * Sales/Book Value * (1 - Payout ratio)

= .1784 * Sales/Book Value * (1 - 0.45) = 11%

Sales/Book Value = 1.12

New Growth Rate (for high growth period)

= .1429 * 1.12 * (1 - 0.45) = 8.81%

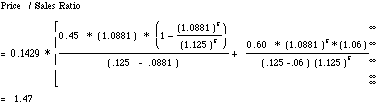
Question 5

A.

Next 10 Years

After Year 10

Payout Ratio

33.00%

60.00%

Sales/Book Value

2.50

2.50

Expected Growth Rate

16.75%

6.00%

Cost of Equity

14.15%

12.50%

Profit Margin

10.00%

10.00%

P/S Ratio =

1.59991143

Price per share =

$39.00

B.

Next 10 Years

After Year 10

Payout Ratio

33.00%

60.00%

Sales/Book Value

3.00

3.00

Expected Growth Rate

16.08%

6.00%

Cost of Equity

14.15%

12.50%

Profit Margin

8.00%

8.00%

P/S Ratio =

1.21549194

Price Per Share =

$35.55

C. The status quo strategy is best, since it leads to a higher price per share.

D. Sales would have to drop 20%. (Sales/book value ratio would have to be 2.40 for the two strategies to be equivalent.)

Question 6

A. The coefficients on this regression measure both the direction and the magnitude of the relationship between P/S ratios and independent variables. My concerns would be the same as for the peer group regression.

B.

Company

P/S Ratio

Profit

Margin

Payout

Exp. Growth

Beta

Predicted

P/S

Arbor Drugs

0.42

3.40%

18%

14.00%

1.05

0.39904

Big B Inc.

0.30

1.90%

14%

23.50%

0.70

0.48704

Drug Emporium

0.10

0.60%

0%

27.50%

0.90

0.28121

Fay's Inc.

0.15

1.30%

37%

11.50%

0.90

0.34188

Genovese

0.18

1.70%

26%

10.50%

0.80

0.37292

Longs Drug

0.30

2.00%

46%

6.00%

0.90

0.38680

Perry Drugs

0.12

1.30%

0%

12.50%

1.10

0.14108

Rite Aid

0.33

3.20%

37%

10.50%

0.90

0.48487

Walgreen

0.60

2.70%

31%

13.50%

1.15

0.33992

These predictions use the information in the entire cross-section, and should be more reliable.

C. P/S = 0.42 + 0.33 * 0 + 0.73 * 0.20 - 0.43 * 0.93 + 7.91 * 0.06

= 0.64

The values in this regression are the values of the private firm being valued.

Market Value of Equity = Revenues * Price/Sales Ratio

= 250 * 0.64 = $160 million

CHAPTER 17 - SOLUTIONS

OPTION PRICING THEORY

Question 1

A. The values of the option parameters are as follows:

S = $83

K = $85

t = 0.25

r = 3.80%

Variance = 0.09

Value of call = $4.42

B. To replicate this call, you would have to:

Buy 0.4919 Shares of Stock (this is N(d1) from the model)

and

Borrow K e-rt N(d2) = 85 exp-(0.038)(0.25) (0.4324) = $36.40

C. At an implied variance of 0.075, the call has a value of approximately $4.00 (the market price).

Implied Standard Deviation = 0.2739

D.


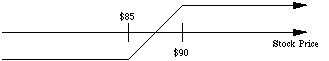
E.

Value of Three-month Put = C - S + Ke-rt = $4.42 - $83 + 85 exp-(0.038)(0.25) = $5.62

Question 2

A. S = $28.75

K = $30

t = 0.25

r = 3.60%

s2 = 0.04

PV of Expected Dividends = $0.28/(1.036)2/12 = $0.28

Value of Call = $0.64

B. The payment of a dividend reduces the expected stock price, and hence reduces the value of calls and increases the value of puts.

Question 3

A. First value the three-month call, as above:

Value of Call = $0.64

Then, value a call to the first (and only) dividend payment,

S = $28.75

K = $30

t = 2/12

r = 3.60%

s2 = 0.04

y = 0 (since it assumes exercise before the dividend payment)

Value of Call = $0.51

Since the value of the three-month call is higher, there is no anticipated exercise.

B. If the dividend payment is large enough, it may pay to exercise the call just before the ex-dividend day (before the stock price drops) rather than wait until expiration. This early exercise is more likely for call options:

(a) the larger the dividend on the stock, and

(b) the closer the option is to expiration.

Question 4

A. You would need to borrow Ke-rt N(d2) = 90 exp(-0.04)(0.25) (0.4500) = $40.10

B. You would need to buy 0.575 shares of stock.

Question 5

A. S= $4.00

K = $4.25

r = 5%

t = 1

Variance = 0.36

Value of Warrant = $0.93

B. Adjusted Stock Price = (Stock Price * Number of Shares Outstanding) + (Warrant price * Number of Warrants Outstanding)/(Number of Shares+Number of Warrants)

= ($4.00 * 11,000,000 + $0.93 * 550,000)/(11,550,000) = $3.85

(To avoid the circular reasoning problem, the price from the no-dilution case is used.)

Adjusted Exercise Price = $4.25

r = 5%

t = 1

Variance = 0.36

Value of Warrant = $0.80

(If you are using a spreadsheet with iterations turned on, and are feeding the option prices back to calculate the adjusted stock price, the value of the warrants is still $0.80.)

C. Dilution increases the number of shares outstanding. For any given value of equity, each share is worth less.

Question 6

A. S = 250

K = 275

t = 5

r = 5%

s2 = (0.15)2

y = 0.03

Value of call = $29.09

B. Value of put with same parameters = $28.09

C.

(1) The variance will be unchanged for the life of the option. This is likely to be violated because stock price variances do change substantially over time.

(2) There will be no early exercise. This is reasonable and is unlikely to be violated.

(3) Any deviations from the option value will be arbitraged away.

While there are plenty of arbitrageurs eager to exploit deviations from true value, arbitraging an index is clearly more difficult to do than arbitraging an individual stock.

Question 7

New Security = AT & T stock - Call (K=60) + Put (K=45)

= $50 - $2.35 + $3.55 = $51.20

The call with a strike price of $60 is sold, eliminating upside potential above $60.

The put with a strike price of $45 is bought, providing downside protection.

CHAPTER 18 - SOLUTIONS

APPLICATIONS OF OPTION PRICING THEORY TO VALUATION

Question 1

A. Value of the firm = 40 (1-0.4)/(.10-.05) = $480 million

B. S = $480

K = $500

t = 5 years

r = 5%

s=0.125

Note: Since the dividends are paid to the stockholders, and we are valuing equity, it is not shown as a dividend yield.

Value of Call (Equity) = $106.39

C. Value of Debt = $480 - $106.39 = $373.61 million

Appropriate Interest Rate = (500/373.61)(1/5) - 1 = 6.00%

Question 2

A. Firm Value

B. Standard Deviation of Firm

= [(0.67)2(0.35)2 + (0.33)2 (0.15)2 + 2 (0.67)(0.33) (.5) (.35) (.15)

= 0.2619

S = 19,883.21 r=5%

K = FV of Debt = 10,000 Variance = 0.26192 = 0.0686

t = Average Duration of Debt = 3 Dividend Yield = 0

d1 = 2.07 N(d1) = 0.9808

d2 = 1.62 N(d2) = 0.9472

Value of Call (Equity) = $11,350

C. Market Value of Equity = $12,200

Implied Variance = 0.25

Implied Standard Deviation = 0.5

D. Market Value of Debt = $8,534

Question 3

A. PV of Inflows = 400,000 * 0.85 * (1 - 1.0425/1.0725)/(.07 - .04) -400,000 * 0.40 * (1 - 1.0325/1.0725)/(.07 - .03) = $3,309,756

Fixed Costs associated with opening

= -3,000,000

NPV = 3,309,756 -3,000,000 = $309,756

B. S = 3,309,756

K = 3,000,000

t = 25

r = 7%

s = 0.25

y = 1/25 = 4%

Value of the Call Option = $828,674

C. The latter considers the option characteristics of owning the mine, i.e., that copper prices may go up, and is higher.

Question 4

Current Value of Developed Reserve

= 10,000,000 * ($20 - $6) = $140,000,000

Exercise Price = Cost of Developing Reserve = $120,000,000

t = 20 years

r = 7%

s = 20%

y = 4%

Value of Call (Natural Resource Reserve) = $37,360,435

Question 5

A. NPV of Project = $250 - $200 = $50 million

B. The option has the following characteristics:

S = 250

K =200

r = 8%

t = 5

Variance = 0.04

Dividend Yield = 12.5/250 = 5%

Value of Call (Project Rights) = $68.68

C. The latter captures the value of delaying the project. The difference between the two values will increase as the variance in the project cash flows increases.

Question 6

A. S = PV of Cash Inflows on Project = 250

K = Cost of Taking Project = 500

t = 10 years

r = 6%

s = 0.6

y = 10/250 = 4%

Value of Call (Product Patent) = $95 million

B. It is an increasing function of the variance in project cash flows. This analysis suggests that the rights to products in technologically volatile areas are likely to be worth a great deal, even though the products may not be viable now.

CHAPTER 19 - SOLUTIONS

THE DETERMINANTS OF INTEREST RATES

Problem 1

Semi-annual coupon = $40

Maturity of the bond = 20

PV of Bond at 9% rate = $40(PVA,4.5%,40)+ $1000/1.045^20 = $ 907.99

Present Value of Bond at 11% annual rate = $ 759.31

Percentage Change in Price = (759/908)-1 = -16.38%

PV of Bond at 7% annual rate = $ 1,106.78

Percentage Change in Price = (1107/908)-1 = 21.89%

 

Problem 2

Semi-annual coupon =$37.50

Maturity = 12 years

PV of Bond at 8% interest rate = $ 961.88

Add accrued interest = $ 37.50/1.08^(1/4)= $ 36.79

Value of Bond = $ 998.67

 

Problem 3

Year (t)

Cash Flow

PV

PV * t

1

100

$ 92.59

$ 92.59

2

100

$ 85.73

$ 171.47

3

100

$ 79.38

$ 238.15

4

100

$ 73.50

$ 294.01

5

1100

$ 748.64

$ 3,743.21

$ 1,079.85

$ 4,539.43

Duration = 4539.43/1079.85 = 4.20

 

Problem 4

Longer term bonds are more sensitive to changes in interest rates, because they have higher duration. Another way of putting this is that the largest cash flow on a longer term bond, i.e., the principal payment, occurs further out in the future. The present value effect is greater the further into the future a cash flow occurs.

The same reasoning applies for zero coupon versus coupon bonds. Zero coupon bonds have only one cash flow - the principal payment, whereas coupon bonds have cash flows over their lifetime.

 

Problem 5

Expected Real Rate of Return = 1.08/1.05 - 1 = 2.86%

The actual return may be different because the actual inflation rate might be higher than or lower than the expected rate.

 

Problem 6

Maturity

Yield to Maturity

1 year

5.00%

2 years

5.50%

3 years

6.00%

4 years

6.50%

5 years

7.00%

a. Yield curve will have yields to maturity as spot interest rates.

b.

Maturity

Spot Rate

1

5.000%

2

5.514%

: 100 = 5.5/1.05 + 105.5/(1+r)^2

3

6.041%

: 100 = 6/1.05+6/1.05514^2+ 106/(1+r)^3

4

6.585%

5

7.152%

c.

Maturity

Forward Rate

1

5.000%

2

6.002%

: (1.055^2-1.05)-1

3

7.007%

:(1.06^3/1.055^2)-1

4

8.014%

5

9.024%

 

Problem 7

The yield curve is driven by two variables - liquidity premiums (if any) and expectations

about future interest rates. If investors expect interest rates to come down (either because

inflation or real rates are anticipated to decrease), you can still have downward sloping

yield curves with positive liquidilty premiums.

 

Problem 8

No. For two reasons. First, given the higher default risk over the time period, I would have expected to make a higher return even after adjusting for the default rate. Second, the period under consideration is a fairly short one. It is entirely possible that a major crisis

in a later period could wipe out much of the perceived excess returns from this period.

CHAPTER 20 - SOLUTIONS

SPECIAL FEATURES IN BONDS

Problem 1

a. Conversion Ratio = $ 30.00

Conversion Price = 30 * 27 = $ 810.00

b. Conversion Premium = 1177-810 = $ 367.00

Value of Straight Bond component = $ 20 (PVA,4%,40) + 1000/1.04^40 = $ 604.14

c. Value of Conversion Option = $ 1177 - 610 = $ 567.00

 

Problem 2

a. Value of Conversion Option:

S = $15; K = 1000/50=$20; t=15; r= 9% (used riskless rate < 10%); Std Dev=0.4;

Value of Conversion Option = $ 9.21 * 50 = $ 460.50

(I assumed a 9% riskless rate, a zero dividend yield and allowed for dilution)

b. Value of Straight Bond = 50 (PVA, 10%,15) + 1000/1.1^15

= $ 619.70

c. Total Value of Convertible Bond = $ 460.5+ $ 619.70

= $ 1,080.20

If issued at par, the company would be losing $ 80 per convertible bond

d. Forced conversion would lower the value of these bonds.

 

Problem 3

a. False. Callable bonds will sell for less than non-callable bonds.

b. True.

c. True

d. False. The non-callable bond will be more sensitive.

 

Problem 4

Yield to Maturity: 45/(1+r/2)^20+1000/(1+r/2)^20 = 950

Solving for r, YTM = 9.80%

 

Yield to Call: 45/(1+r/2)^6+1100/(1+r/2)^6 = 950

Solving for r, YTM = 13.90%

 

I would use the lower of the two numbers

 

Problem 5

a. If investors wait too long to prepay, the actual returns will exceed the expected returns.

b. If investors prepay when rational, the actual returns should equal expected returns.

 

Problem 6

a. True

b. True. It has less upside potential.

c. False. It has less downside risk.

d. True. It is less risky.

CHAPTER 21 - SOLUTIONS

VALUING FUTURES CONTRACTS

1. The implied interest rate can be calculated by dividing the futures price by the spot price.

Implied interest rate= (Futures price/ Spot price) - 1

Months to expiration

Trading at

Futures/Spot

Annualized

1

$404.62

0.3397%

4.1539%

2

$406.11

0.7092%

4.3316%

3

$407.70

1.1035%

4.4877%

6

$412.51

2.2963%

4.6454%

12

$422.62

4.8035%

4.8035%

2a. Theory Price= Spot price + Spot price (Int rate- Div. Yield)

= 258.90 + 258.90 (1.06^(164/365)-1.03^(164/365)) = 262.306356

The actual price is lower than the theory price. The contract is underpriced.

To set up the arbitrage: (1) Buy futures contract (2) Sell short stocks in index (3) Invest in T.Bills

 

2b. Sell futures contracts on the index. # of contracts= (380000/258.90)*0.8/500= 2.34839706

 

3. # of contracts that have to be sold= (100 mil/258.9)*1.25/500= 965.623793

3b. Expected Return on the mutual fund= 6+ 1.25(8)= 16%

3c. Expected return if you hedge away all market risk= 6% (Riskfree rate)

 

4. Theory price= Spot price (1+r) +kt = 481.40(1.06)+ 481.40(.02)= 519.912

Actual price= 515.60. The contract is underpriced.

To set up arbitrage:(1) Buy futures contract (2) Sell short on gold (3) Invest in T.Bills

To unwind: (1) Collect on T.Bills (2) Pay 515.60. Receive gold (3) Return gold; Collect storage cost;

Net profit= 519.91-515.60= 4.31

 

5a.

Month

Theory Basis

Actual Basis

March

1.26668689

0.43

Underpriced

June

3.03339624

1.93

Underpriced

5b. To set up arbitrage:(1) Buy futures contract (2) Sell short on stocks (3)Invest in T.Bills

At expiration: (1)Collect on T.Bills (2) Pay $247.75; Receive stocks. (3) Deliver stocks; Pay dividends;

6a.

a. F* = Spot (1+r)^t + kt = 19000 (1.10) + 200 = 21,100

b. Since the actual futures contract price is $20,400, I would

1. Buy the futures contract for $20,400

2. Sell short wheat at $ 19,000

3. Invest the cash at 10%

At expiration:

1. Collect on my cash investment = $ 20,900

2. Take delivery on the futures contract paying $ 20,400

3. Return the wheat to the owner; collect saved storage costs of $ 200

Arbitrage Profit = (20,900+200) - 20,400 = $ 700

c. 19,000 (1+r) = 20,400

Solve for r,

r = 20,400/19000 = 7.37%

 

CHAPTER 22 - SOLUTIONS

REAL ESTATE VALUATION

Problem 1

The beta estimated by this analyst is probably too low because &endash;

(a) appraised values tend to be smoothed out relative to the market values of real estate

(b) the stock index was used as the market portfolio instead of an index including all assets

 

Problem 2

While REITs have more reliable market prices than the appraised series, the betas estimated

using REITs will still have the following problems

(a) The process of securitizing real estate (in REITs) may affect their risk characteristics

(b) REITs operate under significant legal restrictions on investment, financing and dividend

policy, all of which may affect the beta.

(c) Finally, the stock index is still the inappropriate market index, if one's objective is to

measure the market risk.

 

Problem 3

Commercial Real Estate in New York: Financial Service Firms

Commercial Real Estate in Houston: Oil Service Firms

Commerical Real Estate in San Jose: Computer Software Firms

Hotel Complex in Orlando: Theme Parks (eg. Disney) and Tourism

 

Problem 4

The assessed risk is likley to include some real-estate specific risk if the investors are all

primarily real estate. If the investors are all institutional investors, the only risk that

matters is market risk or risk that cannot be diversified in a portfolio including financial

and real assets.

 

Problem 5

I would do a traditional discounted cash flow valuation of the property and then apply a

liqudity discount which will be higher for more illiquid assets.

Problem 6

1

2

3

4

5

6

Revenues

$ 3,307,500

$ 3,969,000

$ 4,688,381

$ 4,922,800

$ 5,168,940

$ 5,324,009

- Var. Oper. Exp.

$ 945,000

$ 992,250

$ 1,041,863

$ 1,093,956

$ 1,148,653

$ 1,183,113

- Fixed Exp.

$ 309,000

$ 318,270

$ 327,818

$ 337,653

$ 347,782

$ 358,216

- RE Taxes

$ 300,000

$ 309,000

$ 318,270

$ 327,818

$ 337,653

$ 347,782

Taxable Income

$ 1,753,500

$ 2,349,480

$ 3,000,431

$ 3,163,374

$ 3,334,852

$ 3,434,898

- Taxes

$ 736,470

$ 986,782

$ 1,260,181

$ 1,328,617

$ 1,400,638

$ 1,442,657

Ope. Inc after tax

$ 1,017,030

$ 1,362,698

$ 1,740,250

$ 1,834,757

$ 1,934,214

$ 1,992,241

Terminal Value

$ 48,597,161

PV at 7.10%

$ 949,612

$ 1,188,023

$ 1,416,607

$ 1,394,533

$ 35,861,124

Value of Building = $40,809,899

Cost of Capital = 12.5% (.3) + 8.25% (1-.42) (.7) =

b. Value of Equity in Building = $ 40,809,899 - .7($40,809,899) = $ 12,242,970

(I am assuming that there is no depreciation.)

Problem 7

Property

Sale Price

Size (Sq. Ft)

Gross Rent

Sales/sq foot

Price/Rent

A

$20,000,000

400,000

$5,000,000

50.00

4.00

B

$18,000,000

425,000

$4,750,000

42.35

3.79

C

$22,000,000

450,000

$5,100,000

48.89

4.31

D

$25,000,000

400,000

$5,500,000

62.50

4.55

E

$15,000,000

350,000

$4,000,000

42.86

3.75

F

$12,000,000

300,000

$3,000,000

40.00

4.00

Average

47.77

4.07

a. Value based on Sales/sq foot = 300,000 * 47.77 = $14,331,000

b. Value based upon Price/Rent = (300,000 * 1.05 * $ 15 * .7) * 4.07 = $13,461,525

c. We are assuming that the comparable buildings are fairly priced and are similar to the building being valued.