A
Primer on Statistics
Large amounts of data are often compressed into more easily assimilated summaries, which provide the user with a sense of the content, without overwhelming him or her with too many numbers. There a number of ways in which data can be presented. One approach breaks the numbers down into individual values (or ranges of values) and provides probabilities for each range. This is called a "distribution". Another approach is to estimate "summary statistics" for the data. For a data series, X1, X2, X3, ....Xn, where n is the number of observations in the series, the most widely used summary statistics are as follows –
• the mean (m), which is the average of all of the observations in the data series
![]()
• the median, which is the mid-point of the series; half the data in the series is higher than the median and half is lower
• the variance, which is a measure of the spread in the distribution around the mean, and is calculated by first summing up the squared deviations from the mean, and then dividing by either the number of observations (if the data represents the entire population) or by this number, reduced by one (if the data represents a sample)
![]()
When there are two series of data, there are a number of statistical measures that can be used to capture how the two series move together over time. The two most widely used are the correlation and the covariance. For two data series, X (X1, X2,.) and Y(Y,Y... ), the covariance provides a non-standardized measure of the degree to which they move together, and is estimated by taking the product of the deviations from the mean for each variable in each period.
![]()
The sign on the covariance indicates the type of relationship that the two variables have. A positive sign indicates that they move together and a negative that they move in opposite directions. While the covariance increases with the strength of the relationship, it is still relatively difficult to draw judgements on the strength of the relationship between two variables by looking at the covariance, since it is not standardized.
The correlation is the standardized measure of the relationship between two variables. It can be computed from the covariance –

The correlation can never be greater than 1 or less than minus 1. A correlation close to zero indicates that the two variables are unrelated. A positive correlation indicates that the two variables move together, and the relationship is stronger the closer the correlation gets to one. A negative correlation indicates the two variables move in opposite directions, and that relationship also gets stronger the closer the correlation gets to minus 1. Two variables that are perfectly positively correlated (r=1) essentially move in perfect proportion in the same direction, while two assets which are perfectly negatively correlated move in perfect proportion in opposite directions.
A simple regression is an extension of the correlation/covariance concept. It attempts to explain one variable, which is called the dependent variable, using the other variable, called the independent variable. Keeping with statistical tradition, let Y be the dependent variable and X be the independent variable. If the two variables are plotted against each other on a scatter plot, with Y on the vertical axis and X on the horizontal axis, the regression attempts to fit a straight line through the points in such a way as the minimize the sum of the squared deviations of the points from the line. Consequently, it is called ordinary least squares (OLS) regression. When such a line is fit, two parameters emerge – one is the point at which the line cuts through the Y axis, called the intercept of the regression, and the other is the slope of the regression line.

OLS Regression: Y = a + b X
The slope (b) of the regression measures both the direction and the magnitude of the relation. When the two variables are positively correlated, the slope will also be positive, whereas when the two variables are negatively correlated, the slope will be negative. The magnitude of the slope of the regression can be read as follows - for every unit increase in the dependent variable (X), the independent variable will change by b (slope). The close linkage between the slope of the regression and the correlation/covariance should not be surprising since the slope is estimated using the covariance –
![]()
The intercept (a) of the regression can be read in a number of ways. One interpretation is that it is the value that Y will have when X is zero. Another is more straightforward, and is based upon how it is calculated. It is the difference between the average value of Y, and the slope adjusted value of X.
![]()
Regression parameters are always estimated with some noise, partly because the data is measured with error and partly because we estimate them from samples of data. This noise is captured in a couple of statistics. One is the R-squared of the regression, which measures the proportion of the variability in Y that is explained by X. It is a direct function of the correlation between the variables –
![]()
An R-squared value closer to one indicates a strong relationship between the two variables, though the relationship may be either positive or negative. Another measure of noise in a regression is the standard error, which measures the "spread' around each of the two parameters estimated- the intercept and the slope. Each parameter has an associated standard error, which is calculated from the data –
Standard Error of Intercept = SEa =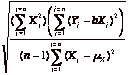

If we make the additional assumption that the intercept and slope estimates are normally distributed, the parameter estimate and the standard error can be combined to get a "t statistic" that measures whether the relationship is statistically significant.
T statistic for intercept = a/SEa
T statistic from slope = b/SEb
For samples with more than 120 observations, a t statistic greater than 1.66 indicates that the variable is significantly different from zero with 95% certainty, while a statistic greater than 2.36 indicates the same with 99% certainty. For smaller samples, the t statistic has to be larger to have statistical significance.[1]
The regression that measures the relationship between two variables becomes a multiple regression when it is extended to include more than one independent variables (X1,X2,X3,X4..) in trying to explain the dependent variable Y. While the graphical presentation becomes more difficult, the multiple regression yields a form that is an extension of the simple regression.
Y = a + b X1 + c X2 + dX3 + eX4
The R-squared still measures the strength of the relationship, but an additional R-squared statistic called the adjusted R squared is computed to counter the bias that will induce the R-squared to keep increasing as more independent variables are added to the regression. If there are k independent variables in the regression, the adjusted R squared is computed as follows –


In theory, the independent variables in a regression need to be uncorrelated with each other. In practice, they often are, and this correlation across independent variables is called multi-collinearity. When there is multi-collinearity,
· The coefficients on each of the independent variables becomes much more difficult to read in isolation, since variables start proxying for each other.
· The reported t-statistics tend to overstate the significance of the relationship. There are statistical approaches available for dealing with multi-collinearity.
· The regression still has predictive power
Both the simple and the multiple regression are based upon a linear relationship between the dependent variable and the independent variable. When the relationship is non-linear, using a linear regression will yield incorrect predictions. In such cases, the independent variables will need to be transformed to make the relationship more linear.
