Empirical Evidence
As the studies of the time series
properties of prices have proliferated, the evidence can be classified into two
classes - studies that focus on short-term (intraday, daily and weekly price
movements) price behavior and research that examines long-term (annual and
five-year returns) price movements. Since the findings are contradictory, we will present them
separately. We will also present evidence on seasonal patterns in stock prices
that seem to persist not only over many periods but across most markets.
a. Short Term Price Patterns
The
notion that today's price change conveys information about tomorrow's price
change is deep rooted in most investors' psyches. In its more sophisticated
formats, the notion that there are patterns in price movements over short
periods of time forms the basis for much of charting. All to often, these
patterns are backed up anecdotal evidence, with the successful experiences on
one or a few stocks extrapolated to form rules about all stocks and assets.
Even in a market that follows a perfect random walk, you will see price
patterns on some stocks that seem to defy probability. The entire market may go
up ten days in a row, or down, for no other reason than pure chance. Given that
this is often true, how do we test to see if there are significant price
patterns? We will consider two ways
in which researchers have examined this question in this section.
a. Serial correlation
If
today is a big up day for a stock, what does this tell us about tomorrow? There
are three different points of view. The first is that the momentum from today
will carry into tomorrow, and that tomorrow is more likely to be an up day than
a down day. The second is that there will be the proverbial profit taking as
investors cash in their profits and that the resulting correction will make it
more likely that tomorrow will be a down day. The third is that each day we
begin anew, with new information and new worries, and that what happened today
has no implications for what will happen tomorrow.
Statistically, the serial
correlation measures the relationship between price changes in consecutive time
periods, whether hourly, daily or weekly, and is a measure of how much the
price change in any period depends upon the price change over the previous time
period. A serial correlation of zero would therefore imply that price changes
in consecutive time periods are uncorrelated with each other, and can thus be
viewed as a rejection of the hypothesis that investors can learn about future
price changes from past ones. A serial correlation that is positive, and
statistically significant, could be viewed as evidence of price momentum in
markets, and would suggest that returns in a period are more likely to be
positive (negative) if the prior period's returns were positive (negative). A
serial correlation which is negative, and statistically significant, could be
evidence of price reversals, and would be consistent with a market where
positive returns are more likely to follow negative returns and vice versa.
From
the viewpoint of investment strategy, serial correlations can sometimes be
exploited to earn excess returns. A positive serial correlation would be
exploited by a strategy of buying after periods with positive returns and
selling after periods with negative returns. A negative serial correlation
would suggest a strategy of buying after periods with negative returns and
selling after periods with positive returns. Since these strategies generate
transactions costs, the correlations have to be large enough to allow investors
to generate profits to cover these costs. It is therefore entirely possible
that there be serial correlation in returns, without any opportunity to earn
excess returns for most investors.
The
earliest studies[1] of serial
correlation all looked at large U.S. stocks and concluded that the serial
correlation in stock prices was small. One of the first by Fama in 1965, for
instance, found that 8 of the 30 stocks listed in the Dow had negative serial
correlations and that most of the serial correlations were less than 0.05.
Other studies confirm these findings Ð of very low correlation, positive or
negative - not only for smaller stocks in the United States, but also for other
markets. For instance, Jennergren and Korsvold (1974) report low serial
correlations for the Swedish equity market and Cootner (1961) concludes that
serial correlations are low in commodity markets as well. While there may be
statistical significance associated with some of these correlations, it is
unlikely that there is enough correlation in short-period returns to generate
excess returns, after you adjust for transactions costs.
The
serial correlation in short period returns is affected by market liquidity and
the presence of a bid-ask spread. Not all stocks in an index are liquid, and,
in some cases, stocks may not trade during a period. When the stock trades in a
subsequent period, the resulting price changes can create positive serial
correlation. To see why, assume that the market is up strongly on day 1, but
that three stocks in the index do not trade on that day. On day 2, if these
stocks are traded, they are likely to go up to reflect the increase in the
market the previous day. The net result is that you should expect to see
positive serial correlation in daily or hourly returns in illiquid market
indices. The bid-ask spread creates a bias in the opposite direction, if
transactions prices are used to compute returns, since prices have a equal
chance of ending up at the bid or the ask price. The bounce that this induces
in prices will result in negative serial correlations in returns.[2]
For very short return intervals, this bias induced in serial correlations might
dominate and create the mistaken view that price changes in consecutive time
periods are negatively correlated.
There
are some recent studies that find evidence of serial correlation in returns
over short time periods, but the correlation is different for high volume and
low volume stocks. With high volume stocks, stock prices are more likely to
reverse themselves over short periods, i.e., have negative serial correlation.
With low volume stocks, stock prices are more likely to continue to move in the
same direction Ð i.e., have positive serial correlation.[3]
b. Runs Tests
Once
in a while a stock has an extended run where stock prices go up several days in
a row or down several days in a row. While this, by itself, is completely
compatible with a random walk, you can examine a stockÕs history to see if
these runs happen more frequently or less frequently than they should. A runs
test is based upon a count of the number of runs, i.e., sequences of price
increases or decreases, in price changes over time. Thus, the following time
series of price changes, where U is an increase and D is a decrease would
result in the following runs -
UUU
DD U DDD UU DD U D UU DD
U DD UUU DD UU D UU D
There were 18 runs in this price series of 33 periods. The
actual number of runs in the price series is compared against the number that
can be expected[4] in a series
of this length, assuming that price changes are random. If the actual number of
runs is greater than the expected number, there is evidence of negative
correlation in price changes. If it is lower, there is evidence of positive correlation.
A study of price changes in the Dow 30 stocks, assuming daily, four-day,
nine-day and sixteen day return intervals provided the following results -
DIFFERENCING
INTERVAL
Daily Four-day Nine-day Sixteen-day
Actual
runs 735.1 175.7 74.6 41.6
Expected runs 759.8 175.8 75.3 41.7
The actual number of runs in four
day returns (175.8) is almost exactly what you would expect in a random
process. Tthere is slight evidence of positive correlation in daily returns but
no evidence of deviations from normality for longer return intervals.
Again,
while the evidence is dated, it serves to illustrate the point that long
strings of positive and negative changes are, by themselves, insufficient
evidence that markets are not random, since such behavior is consistent with
price changes following a random walk. It is the recurrence of these strings
that can be viewed as evidence against randomness in price behavior.
b. Long Term Price Patterns
While
most of the earlier studies of price behavior focused on shorter return
intervals, more attention has been paid to price movements over longer periods
(six months to five-year) in recent years. Here, there is an interesting
dichotomy in the results. When long term is defined as months rather than
years, there seems to be a tendency towards positive serial correlation.
Jegadeesh and Titman present evidence of what they call Òprice momentumÓ in
stock prices over time periods of up to eight months Ð stocks that have gone up
in the last six months tend to continue to go up whereas stocks that have gone
down in the last six months tend to continue to go down. The momentum effect is
just as strong in the European markets, though it seems to be weaker in
emerging markets.[5] What may
cause this momentum? One potential explanation is that mutual funds are more
likely to buy past winners and dump past losers, thus generating price
continuity.[6]
However, when long term is defined
in terms of years, there is substantial negative correlation in returns,
suggesting that markets reverse themselves over very long periods. Fama and
French examined five-year returns on stocks from 1941 to 1985 and present
evidence of this phenomenon. They found that serial correlation is more
negative in five-year returns than in one-year returns, and is much more
negative for smaller stocks rather than larger stocks. Figure 7.2 summarizes one-year and five-years serial
correlation by size class for stocks on the New York Stock Exchange.
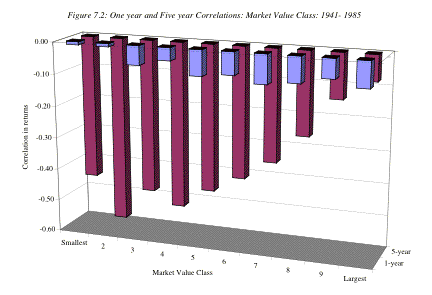
Source: Fama and French (1988)
This phenomenon has also been
examined in other markets, and the findings have been similar. There is
evidence that returns reverse themselves over long time period.
Given
the findings of little or no correlation in the short term and substantial
correlation in the long term, it is interesting that so many technical analysts
focus on predicting intraday or daily prices. The bigger payoff seems to be in
looking at price patterns over much longer periods, though there are caveats we
will present in the next chapter on these long term strategies.
c. Seasonal and Temporal Patterns in Prices
One
of the most puzzling phenomena in asset prices is the existence of seasonal and
temporal patterns in stock prices that seem to cut across all types of asset
markets. As we will see in this section, stock prices seem to go down more on
Mondays than on any other day of the week and do better in January than in any
other month of the year. What is so surprising about this phenomenon, you might
ask? It is very difficult to justify the existence of patterns such as these in
a rational market Ð after all, if investors know that stocks do better in
January than in any other month, they should start buying the stock in December
and shift the positive returns over the course of the year. Similarly, if investors
know that stocks are likely to be marked down on Monday, they are likely to
begin marking them down on Friday and hence shift the negative returns over the
course of the week.
The January Effect
Studies
of returns in the United States and other major financial markets consistently
reveal strong differences in return behavior across the months of the year.
Figure 7.3 reports average returns by month of the year from 1927 to 2001.
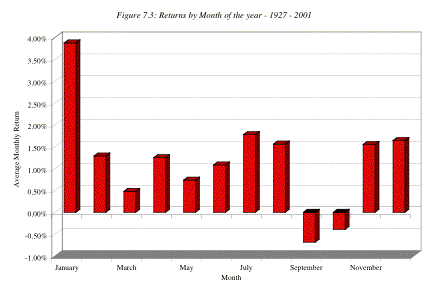
Source: Raw data from French
Returns in January are significantly higher than returns in
any other month of the year. This phenomenon is called the year-end or January
effect, and it can be traced to the first two weeks in January.
The
January effect is much more pronounced for small firms than for larger firms,
and roughly half of the small firm premium, which is the additional return
earned by small firms relative to large firms, is earned in the first few days
of January. Figure 7.4 graphs returns in January by size and risk class for
data from 1935 to 1986.[7]
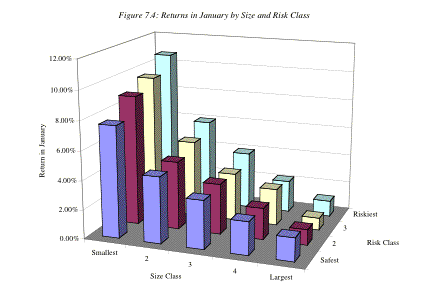
Source: Chopra and Ritter
Note that the January effect is most pronounced for the
smallest, riskiest firms in the market and least pronounced for larger, safer
firms.
A number of explanations have been
advanced for the January effect, but few hold up to serious scrutiny. One is
that there is tax loss selling by investors at the end of the year on stocks
which have gone down to capture the capital gain, driving prices down,
presumably below true value, in December, and a buying back of the same stocks[8]
in January, resulting in the high returns. The fact that the January effect is
accentuated for stocks that have done worse over the prior year is offered as
evidence for this explanation. There are several pieces of evidence that
contradict it, though. First, there are countries, like Australia, which have a
different tax year, but continue to have a January effect. Second, the January
effect is no greater, on average, in years following bad years for the stock
market, than in other years.
A
second rationale is that the January effect is related to institutional trading
behavior around the turn of the years. It has been noted, for instance, that
ratio of buys to sells for institutions drops significantly below average in
the days before the turn of the year and picks to above average in the months
that follow.[9] It is argued
that the absence of institutional buying pushes down prices in the days before
the turn of the year and pushes up prices in the days after. Again, while this may be true, it is not
clear why other investors do not step in and take advantage of these quirks in institutional
behavior.
The
universality of the January effect is illustrated in Figure 7.5 where we
examine returns in January versus the other months of the year in several major
financial markets, and finds strong evidence of a January effect in every
market.[10]
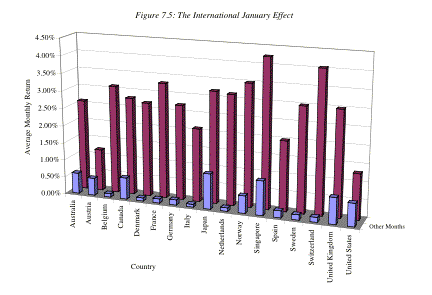
In fact, researchers have unearthed evidence of a January
effect in bond and commodity markets as well.
The Weekend Effect
Are
stock returns consistently higher on some days of the week than others? A
surprising feature of stock returns is the existence of what is called the
weekend effect, another return phenomenon that has persisted over extraordinary
long periods and over a number of international markets. It refers to the
differences in returns between Mondays and other days of the week. The
significance of the return difference is brought out in Figure 7.6, which
graphs returns by days of the week from 1927 to 2001.
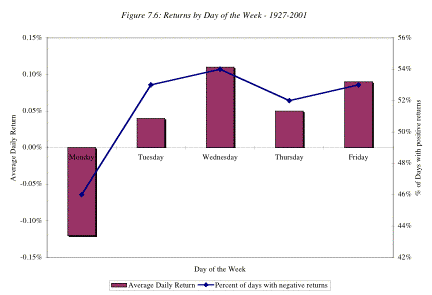The
returns on Mondays are significantly negative, whereas the returns on every day
of the week are not. In addition,
returns on Mondays are negative more often than returns on any other trading
day. There are a number of other findings on the Monday effect that researchers
have fleshed out.
- The
Monday effect is really a weekend effect since the bulk of the negative
returns are manifested in the Friday close to Monday open returns. In
other words, the negative returns on Monday are generated by the fact that
stocks tend to open lower on Mondays than from what happens during the
day. The returns from intraday returns on Monday (the price changes from
open to close on Monday) are not the culprits in creating the negative
returns.
- The
Monday effect is worse for small stocks than for larger stocks. This mirrors our findings on the
January effect.
- The
Monday effect is no worse following three-day weekends than two-day
weekends.
- Monday
returns are more likely to be negative if the returns on the previous
Friday were negative. In fact, Monday returns are, on average, positive
following positive Friday returns, and are negative 80% of the time
following negative Friday returns.[11]
There
are some who have argued that the weekend effect is the result of bad news
being revealed after the close of trading on Friday and during the weekend.
They point to the fact that more negative earnings reports are revealed after
close of trading on Friday. Even if this were a widespread phenomenon, the
return behavior would be inconsistent with a rational market, since rational
investors would build in the expectation of the bad news over the weekend into
the price before the weekend, leading to an elimination of the weekend effect.
The
weekend effect is strong in most major international markets, as shown in
Figure 7.7.
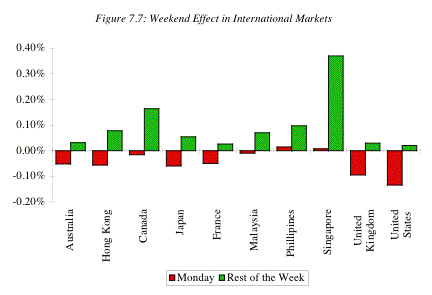The returns on Monday are lower than returns on other days of
the week for every international market examined. The presence of a strong
weekend effect in Japan, which allowed Saturday trading for a portion of the
period studies here indicates that there might be a more direct reason for
negative returns on Mondays than bad information over the weekend.
As
a final note, the negative returns on Mondays cannot be just attributed to the
absence of trading over the weekend. The returns on days following trading
holidays, in general, are characterized by abnormally positive, not negative,
returns. Figure 7.8 summarizes returns on trading days following major holidays
and confirms this pattern.
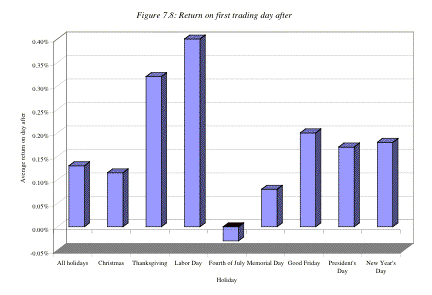
In fact, the returns on the first trading day after a
holiday tend to be much more positive than returns on other trading days.[12]
d. Volume Patters
While
the random walk hypothesis is silent about the relationship between trading
volume and prices, it does assume that all available information is
incorporated in the current price. Since trading volume is part of publicly
available information, there should therefore be no information value to
knowing how many shares were traded yesterday or the day before.
As
with prices, there is evidence that trading volume carries information about
future stock price changes. Datar, Naik and Radcliffe (1998) show that low
volume stocks earn higher returns than high volume stocks, though they
attribute the differential return to a liquidity premium on the former. A more surprising result comes from Lee
and Swaminathan (1998) who look at the interrelationship between price and
trading volume. In particular, they examine the price momentum effect that was documented
by Jegadeesh and Titman Ð that stocks that go up are more likely to keep going
up and stocks that go down are more likely to keep dropping in the months after
- and show that it is much more pronounced for high volume stocks. Figure 7.9 classifies
stocks based upon how well or badly they have done in the last six months
(winners, average and loser stocks) and their trading volume (low, average and
high) and looks at returns on these stocks in the following six months.
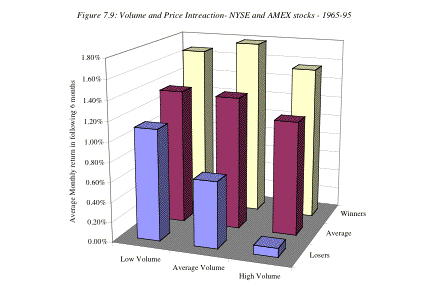
Note that the price momentum effect is strongest for stocks
with high trading volume. In other words, a price increase or decrease that is
accompanied by strong volume is more likely to continue into the next period. Stickel
and Verecchia confirm this result with shorter period returns Ð they conclude
that increases in stock prices that are accompanied by high trading volume are
more likely to carry over into the next trading day.
In
summary, the level of trading volume in a stock, changes in volume and volume
accompanied by price changes all seem to provide information that investors can
use to pick stocks. It is not surprising that trading volume is an integral
part of technical analysis.