
A Variant on Sensitivity Analysis: Scenario Analysis
CAPITAL BUDGETING UNDER UNCERTAINTY
* Alternative approaches to risk adjustment
* Adjust the cash flows to reflect the risk. Be more
conservative in estimating cash flows for riskier ventures and less so for
safer ventures. The danger of this approach is that:
- The risk adjustment will vary from person to person
and from project to project
- There is ample room for preconceptions and biases to
alter the adjustment
- Risk may sometimes be double counted (in the cash flows
as well as the discount rates).
* Allow the decision maker to factor in the risk, when
he (she) makes the decision. For instance, when comparing the NPV of two
projects, the decision maker may choose the one with the lower NPV, because
he (she) feels it is less risky.
* Do what-if analysis on the cash flows, i.e, what would
the NPV be if revenues were 15% greater than or less than expected.
* Adjust the discount rate to reflect the risk.
* Risk adjustment techniques used by respondents
| Technique | % |
| No adjustment is made | 14 |
| Adjustment is made subjectively | 48 |
| Certainty-equivalent method | 7 |
| Risk-adjusted discount rate | 29 |
| Shortening payback period | 7 |
| Others | 5 |
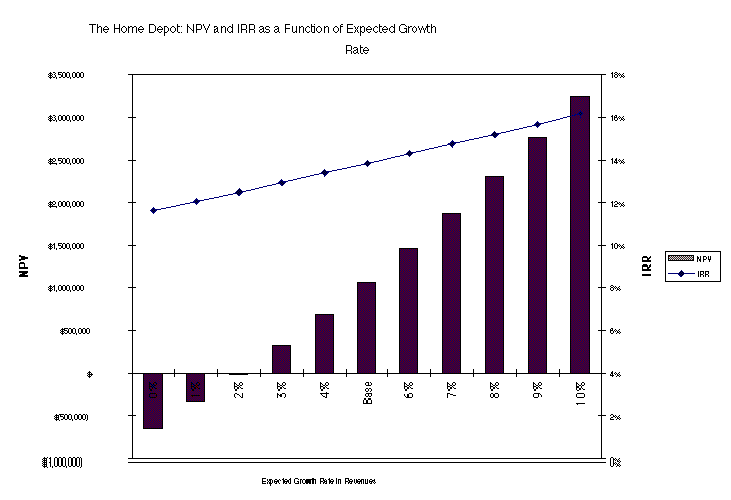
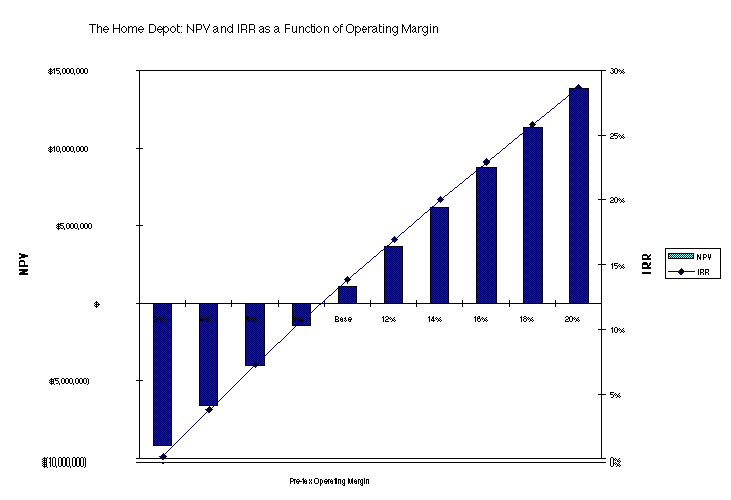
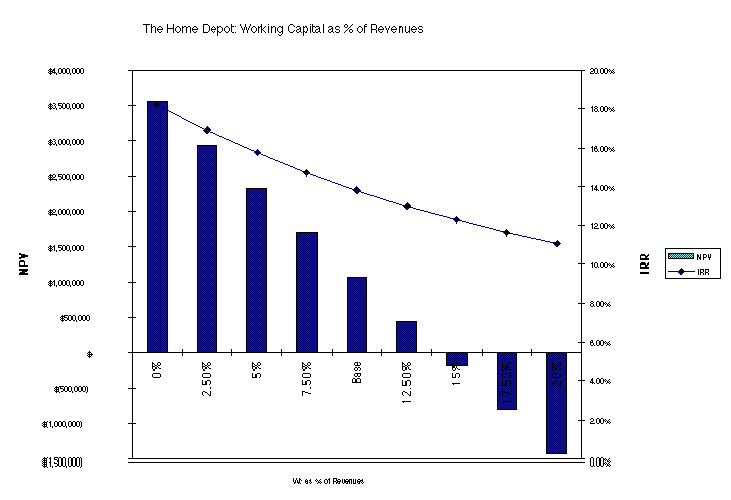
* Sensitivity Analysis
All capital budgeting analyses make assumptions about
future revenues, expenses, salvage value, tax rates and the project lifetime.
Examining the effects of changing each of these variables individually on
the NPV and IRR is sensitivity analysis.
An Example: A Store Analysis for The Home Depot
Base Case Assumptions
Initial Investment in the Store (100,000 squre feet)
= $ 12.5 million
Expected Life of the Store = 10 years
Additional Investment needed at the end of year 5 = $
1 million
Salvage Value of the Store Premises at the end of 10
years = $ 5.5 million
Expected Revenues/Square Foot in first year = $ 300 /
square foot
Pre-tax Operating Margin (EBIT/Sales) = 10.00%
Working Capital as a % of Revenues = 10.00%; Investment
at beginning of each year and completely salvageable at the end of the project
life.
The depreciation each year is computed using ACRS depreciation
rates.
The corporate tax rate is 36.00%; The cost of capital
is 12.5%
Base Case Analysis 7
| Year | Investment | Revenues | EBIT (1-t) | Depreciation | Chg. in WC | FCFF |
| 0 | -12500000 | -3000000 | -15500000 | |||
| 1 | 30000000 | 1920000 | 540000 | -150000 | 2310000 | |
| 2 | 31500000 | 2016000 | 432000 | -157500 | 2290500 | |
| 3 | 33075000 | 2116800 | 345600 | -165375 | 2297025 | |
| 4 | 34728750 | 2222640 | 276480 | -173644 | 2325476 | |
| 5 | -1000000 | 36465188 | 2333772 | 221184 | -182326 | 2372630 |
| 6 | 38288447 | 2450461 | 176947 | -191442 | 2435966 | |
| 7 | 40202869 | 2572984 | 141558 | -201014 | 2513527 | |
| 8 | 42213013 | 2701633 | 113246 | -211065 | 2603814 | |
| 9 | 44323663 | 2836714 | 90597 | -221618 | 2705693 | |
| 10 | 5500000 | 46539846 | 2978550 | 72478 | 4653985 | 13205012 |
FCFF = EBIT (1-t) + Depreciation + Change
in Working Capital
Net
Present Value (at cost of capital of 12.5%)= $ 1,067,099 : Accept the Project
Internal Rate of Return = 13.83% > Cost of Capital
: Accept the Project
Sensitivity Analysis




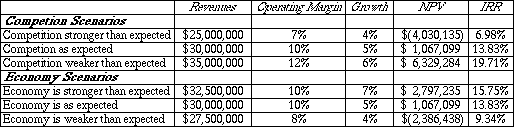
A Variant on Sensitivity Analysis: Scenario Analysis
In scenario analysis, specific scenarios
are defined, with growth and income characteristics under each. The net
present value and internal rates of return for the project are estimated
under each scenario ñ
What next?
* Effects Of Assumptions About Project Lifetime
Consider the following project:
Initial Investment = $1,000,000; Salvage Value after
10 years = $200,000
Initial Working Capital Needs = $100,000; Maintain at
25% of Revenues
Revenues in year 1 = $400,000; Grows at 10% a year;
COGS = 50% of Revenues
Discount rate for project = 15%
| Year | Initial Invest. | Revenues | COGS | BTCF | ATCF | WC Chg | NATCF |
| 0 | -1100000 | ||||||
| 1 | 400000 | 200000 | 200000 | 120000 | 0 | 120000 | |
| 2 | 440000 | 220000 | 220000 | 132000 | 10000 | 122000 | |
| 3 | 484000 | 242000 | 242000 | 145200 | 11000 | 134200 | |
| 4 | 532400 | 266200 | 266200 | 159720 | 12100 | 147620 | |
| 5 | 585640 | 292820 | 292820 | 175692 | 13310 | 162382 | |
| 6 | 644204 | 322102 | 322102 | 193261 | 14641 | 178620 | |
| 7 | 708624 | 354312 | 354312 | 212587 | 16105 | 196482 | |
| 8 | 779487 | 389743 | 389743 | 233846 | 17716 | 216130 | |
| 9 | 857436 | 428718 | 428718 | 257231 | 19487 | 237743 | |
| 10 | 943179 | 471590 | 471590 | 282954 | 21436 | 261518 |
* Monte Carlo Simulations
Step 1: Instead of using an
expected value for each of the inputs, develop probability distributions
for each of the variables.
Example: In the Home Depot
example, assume the following distributions for each of the following variables
ñ
Variable Distribution Expected Value Characteristics
of the Distribution
1. Revenues General $ 30 million Value Probability
$ 20 million 0.125
$ 25 million 0.1875
$ 30 million 0.375
$ 35 million 0.1875
$ 40 million 0.125
2. Growth Rate Normal 5.00% Standard Deviation = 2.00%
3. Operating Margin Uniform 10.00% Minimum of 2.50%
Maximum of 20.00%
4. WC as % of Rev. Normal 10.00% Standard Deviation =
2.50%
Estimation Issues:
How do you choose the right probability distribution?
Step 2: Draw one outcome
from each distribution.
Example: In the Home
Depot example, assume the following drawings ñ
Variable Drawn Outcome
1. Revenues $ 25 million
2. Growth Rate 6.35%
3. Operating Margin 10.00%
4. WC as % of Rev. 9.16%
Estimation Issues:
Step 3: Estimate a
net present value, based upon the outcomes drawn
Example: In the Home
Depot example, calculate the net present value based upon the outcomes drawn
in step 3.
Net Present Value from simulated outcomes = - $13,423
Internal Rate of Return for simulated outcomes = 12.48%
Estimation Issues:
Step 4: Repeat step
2 and 3 a sufficient number of times.
Example: In the Home
Depot example, the simulations were repeated 1000 times. The number was
set to a fairly large number because
Estimation Issues:
Step 5: Compute the
summary statistics for the net present values across all the simulations
(Expected Value, Standard Deviation, Minimum, Maximum, Percent of time under
zero) and plot the net present values on a graph.)
Example: In the Home
Depot example, calculate the summary statistics for net present value based
upon the simulations.
Net Present Value Internal Rate of Return
Expected Value = $ 1,067,150 Expected Value = 13.84%
Standard Deviation = $ 451,335 Standard Deviation = 0.55%
Coeff. of Variation = $ 451,335/1,067,150 CV of IRR =
0.55%/13.84%
Minimum = -$ 9,504,201 Minimum = -1.21%
Maximum = $ 31,013,450 Maximum = 47.95%
% of time below zero = 20.16% % of time below Discount
rate= 20.16%
Step 6: Use the distribution
of net present values, rather than just the base case net present value
to make your decision.
Example: In the Home
Depot example, there are a number of questions that can be answered with
this simulation, including
* Decision Trees
Stage 1: At
t=0, conduct a $500,000 study of market potential.
Stage 2: If it appears that
there is a significant market (assumed to have probability 0.8) at t=1,
spend $1,000,000 to build a small plant to manufacture prototypes for use
in industry.
Stage 3: If the reaction to
the prototypes is good, at t=2, build a larger plant for $10,000,000. The
project is expected to generate cash flows for four years, before the patent
expires.
Assume that the discount rate is 11.5%.
Time Periods
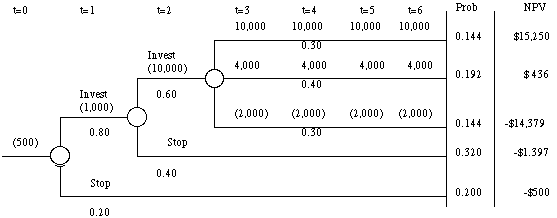
NPV = 0.144* 15,250
+ 0.192 * 436 + 0.144 * (14,379) + 0.32 * 1397 + 0.2* (500)
= - $ 338
Note on calculations:
Probability of best case scenario = 0.8 * 0.6 * 0.4 =
0.144
NPV under best case scenario = - 500 - 1000/1.115 - 10,000/1.1152
+ 10,000/1.1153 +
10,000/1.1154 +
10,000/1.1155 +
10,000/1.1156 =
$15,250
The Abandonment Option
In the example above, assume that you can abandon
the project at the end of t=3, if the cashflows turn out to be negative
(-2,000).
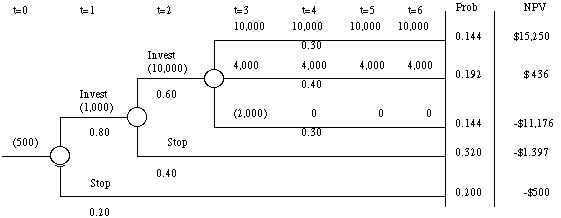
NPV = 0.144* 15,250 + 0.192 * 436 + 0.144 * (11,176)
+ 0.32 * 1397 + 0.2* (500)
= $124