THE CAPM - IN PRACTICE

Using the CAPM in Prediction
There are three inputs needed for the CAPM to yield an expected return -
(a) a Riskfree Rate
(b) a Risk Premium that corresponds to the riskfree rate
(c) a Beta

1. The correct risk free rate to use in the capital asset pricing model

( ) is the short term government security rate

( ) is the long term government security rate

( ) can be either depending upon the purpose of the prediction


A. Riskfree Rate
The riskfree rate that is used in the CAPM can either be -
(a) Short term Government Security Rate: because it has no default or interest rate risk. However, there is 'reinvestment rate' risk if the expected return is used for a long term investment analysis.
(b) Long term Government Bond Rate: because it has no default risk and, if matched to the term of the investment analysis, has no 'reinvestment rate' risk.
B. Risk Premium
The risk premium used in the CAPM is generally based upon historical data. For instance, using the period 1926 to 1988 as the basis, Ibbotson and Sinquefield estimate the following premiums for the United States -
(a) Risk Premium over Government T.Bills: Stocks, on average, have earned an (arithmetic) average premium of 8.5% over the Treasury Bill rate.
Average Return on Stocks - 1926 -1988 = 12.1%
Average Return on T.Bills - 1926-1988 = 3.6%
Risk Premium for Stocks over T.Bills = 8.5%
(b) Risk Premium over Treasury Bonds: Stocks, on average, have earned a (geometric) average premium of 5.5% over the Treasury Bond rate.

 

2. The expected risk premium for investing in the market portfolio is estimated using historical data. This assumes that

( ) Stocks will always do better than T.Bills or T.Bonds

( ) The premium will always be the same

( ) There is no trend in the risk premium, even though it may change over time


C. Beta

The beta to be used in the CAPM is generated by regressing returns on a stock against returns on a market index.

 

Getting Expected Returns: Disney (9/95)

Disney's Current Beta = 1.18 (from Value Line)
Expected Returns:
_ Using T.Bills: T. Bill Rate = 5.5%; Risk Premium = 8.5%;
_ E(RDisney) = 5.5% + 1.18 (8.5%) = 15.53%
_ Using T.Bonds: T.Bond Rate = 6.30%;Risk Premium=5.5%
_ E(RDisney) = 6.30% + 1.18(5.5%) = 12.79%

Disney's Current Price = $57.375
Expected Dividend next year on Disney = $0.35
Using 15.53% as the expected return,
Expected Price 1 year from now = 57.375 (1.1553)-0.35 = $65.94

3. Using the CAPM to make predictions of returns essentially means that there is no room for equity research or stock picking

( ) True

( ) False


What does this expected return tell us?

Investors in stock in Disney
_ need to make 15.53% over the next year to break even
_ long term investors need to make 12.79% annually to break even
_ will decide to invest or not invest in Disney based upon whether they think they can make more or less than this hurdle rate

Managers at Disney
_ need to make at least 12.79% as a return for their equity investors to break even.
_ if they make more than this, they will make their stockholders happy

if they make less, .....

 

4. Managers should try to reduce their stock betas, because that will reduce their costs of equity

( ) True

( ) False



Using The CAPM In Evaluation
Step 1: Get riskfree rate from start of the period for which you want to do the evaluation.
Step 2: Get the beta for the project , company or portfolio you want to evaluate.
Step 3: Get the actual return on the market index for the period for which you want to make the evaluation. (Remember to add back the dividend yield to the actual index appreciation).
Step 4: Estimate return you would have expected to make during the period of the evaluation
E(R j ) = R f + b j (E(R m ) - R f )
Step 5: Estimate actual returns made by project or stock:
Actual return = (Price t -Price t-1 +Dividend t-1 )/Price t-1
Step 6: Compare actual to expected return
Excess return = Actual return - Expected > 0: Positive

Performance Evaluation : Disney (9/94-9/95)

Disney's price increased from $ 39.50 to $ 57.375, and it paid a dividend of $ 0.35.
Data from year ago
_ Disney's Beta = 1.18; T.Bill Rate one year ago = 6.00%;

Return on the market index from 9/94 to 9/95
_ Return on Index (NYSE) = 21.32%

_ Dividend yield on index = 2.80%
_ Total Return on Index = 24.12%

Expected Return on Disney from 9/94 to 9/95
_ 6.00% + 1.18 (24.12% - 6.00%) = 27.38%

Actual Return on Disney : 9/94 to 9/95
_ Price Change from 9/94 to 9/95 = $ 57.375 - $ 39.50 =17.875
_ Dividend paid from 9/94 to 9/95 = $ 0.35
_ Total Return = (17.875+0.35)/ 39.50 = 46.14%

Jensen's Alpha = 46.14% - 27.38% = 18.74%

 

5. You invested in the Quantum Fund, a mutual fund which invests in stocks in high risk and high growth areas one year ago. Over the last year, the fund has gone up almost 30%. The managers claim to have beaten the market, since the stock index went up by only 24.12% over the same period. If the fund had a beta of 2.00, and the risk free rate was 6% a year ago, would you agree.

( ) Yes

( ) No




MEASURING BETAS

Standard Procedures for estimating CAPM parameters

The standard procedure for estimating betas is to regress stock returns (R j ) against market returns (R m ) -
R j = a + b R m
where a is the intercept and b is the slope of the regression.
The slope of the regression corresponds to the beta of the stock, and measures the riskiness of the stock.
The intercept of the regression provides a simple measure of performance during the period of the regression, relative to the capital asset pricing model.
R j = R f + b (R m - R f )
= R f (1-b) + b R m ........... Capital Asset Pricing Model
R j = a + b R m ........... Regression Equation
If a > R f (1-b) .... Stock did better than expected during regression period
a = R f (1-b) .... Stock did as well as expected during regression period
a < R f (1-b) .... Stock did worse than expected during regression period
This is the equivalent of Jensen's alpha.
The R squared (R 2 ) of the regression provides an estimate of the proportion of the risk (variance) of a firm that can be attributed to market risk; the balance (1 - R 2 ) can be attributed to firm specific risk.

6. When doing the regression to estimate betas, the market index that is used should be matched up to the stock being analysed. (NASDAQ stocks should use the NASDAQ index... NYSE stocks..)

( ) Yes

( ) No


RETURNS ON INTEL AND S&P 500

Time period Index Price(Stock) DPS(Stock) Split Factor Index Level Return(Stock) Return(Mkt)
1 1 30.75 1 179.63
2 1 28 1 181.19 -0.0894 0.0087
3 1 27.75 0 1 180.66 -0.0089 -0.0029
4 1 27.5 1 179.83 -0.009 -0.0046
5 1 26.38 1 189.55 -0.0407 0.0541
6 1 26 0 1 191.85 -0.0144 0.0121
7 1 28.25 1 190.92 0.0865 -0.0048
8 1 26 1 188.63 -0.0796 -0.012
9 1 25.75 0 1 182.08 -0.0096 -0.0347
10 1 25.5 1 189.82 -0.0097 0.0425
11 1 28.5 1 202.17 0.1176 0.0651
12 1 29.25 0 1 211.28 0.0263 0.0451
13 1 28.25 1 211.78 -0.0342 0.0024
14 1 27.75 1 226.92 -0.0177 0.0715
15 1 26 0 1 238.9 -0.0631 0.0528
16 1 28.5 1 235.52 0.0962 -0.0141
17 1 27.25 1 247.35 -0.0439 0.0502
18 1 23 0 1 250.84 -0.156 0.0141
19 1 18.25 1 236.12 -0.2065 -0.0587
20 1 23 1 252.93 0.2603 0.0712
21 1 19.5 0 1 231.32 -0.1522 -0.0854
22 1 20.25 1 243.98 0.0385 0.0547
23 1 23 1 249.22 0.1358 0.0215
24 1 21 0 1 242.17 -0.087 -0.0283
25 1 31.25 1 274.08 0.4881 0.1318
26 1 38 1 284.2 0.216 0.0369
27 1 38.5 0 1 289.2 0.0132 0.0176
28 1 47 1 288.36 0.2208 -0.0029
29 1 43.88 1 290.1 -0.0664 0.006
30 1 44 0 1 304.1 0.0027 0.0483
31 1 47.75 1 318.66 0.0852 0.0479
32 1 52.75 1 329.8 0.1047 0.035
33 1 57.75 0 1 321.83 0.0948 -0.0242
34 1 26 1.5 251.79 -0.3247 -0.2176
35 1 21.5 1 230.3 -0.1731 -0.0853
36 1 26.5 0 1 247.08 0.2326 0.0729
37 1 25.5 1 257.07 -0.0377 0.0404
38 1 28.25 1 267.82 0.1078 0.0418
39 1 29.38 0 1 258.89 0.04 -0.0333
40 1 31 1 261.33 0.0551 0.0094
41 1 30.75 1 262.16 -0.0081 0.0032
42 1 36.13 0 1 273.5 0.175 0.0433
43 1 34.75 1 272.02 -0.0382 -0.0054
44 1 28 1 261.52 -0.1942 -0.0386
45 1 27.5 0 1 271.91 -0.0179 0.0397
46 1 24.75 1 278.97 -0.1 0.026
47 1 20.25 1 273.3 -0.1818 -0.0203
48 1 23.75 0 1 277.72 0.1728 0.0162
49 1 26 1 297.47 0.0947 0.0711
50 1 25.75 1 288.86 -0.0096 -0.0289
51 1 26.25 0 1 294.87 0.0194 0.0208
52 1 29 1 309.64 0.1048 0.0501
53 1 32.5 1 320.52 0.1207 0.0351
54 1 29 0 1 317.98 -0.1077 -0.0079
55 1 30.5 1 346.08 0.0517 0.0884
56 1 30 1 351.45 -0.0164 0.0155
57 1 32.25 0 1 349.15 0.075 -0.0065
58 1 33.75 1 340.36 0.0465 -0.0252
59 1 34.75 1 345.99 0.0296 0.0165
60 1 34.5 0 1 353.4 -0.0072 0.0214



REGRESSION STATISTICS AND RISK PARAMETERS

The regression statistics for Intel are as follows -
(a) Slope of the regression = 1.70; This is Intel's beta, based upon returns from 1985 to 1989. Using a different time period for the regression or different return intervals (weekly or daily) for the same period can result in a different beta.
(b) Intercept of the regression = -0.48%; This is a measure of Intel's performance, when it is compared with R f (1-b). The monthly riskfree rate (since the returns used in the regression are monthly returns) between 1985 and 1989 averaged 0.5%, resulting in the following estimate for the performance -
R f (1- b ) = 0.5% (1-1.70) = -0.35%
Intercept - R f (1- b ) = -0.48% - (-0.35%) = -0.13% (rounded off from -0.14%)
This analysis suggests that Intel performed 0.14% worse than expected, where expectations are based upon the CAPM, on a monthly basis between January 1985 and December 1989. Annualized, this is equivalent to Jensen's Alpha.
(c) R squared of the regression = 43.46%; This statistic suggests that 43.46% of the risk (variance) in Intel comes from market sources (interest rate risk, inflation risk ...), and tha the balance of 56.54% of the risk comes from firm-specific components. The latter should be diversifiable, and therefore unrewarded in the CAPM.

7. A high R squared is good, because it means that the firm has very little firm-specific risk.

( ) True

( ) False


An Updated Regression for Intel : 1989 - 1993
The following figure graphs monthly returns on Intel against returns on the S&P 500 index from February 1989 to January 1994.
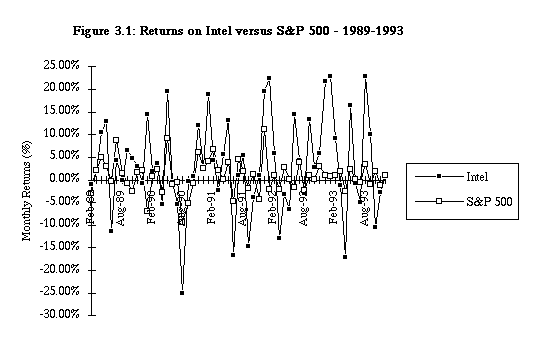
The regression statistics for Intel are as follows -
(a) Slope of the regression = 1.39; This is Intel's beta, based upon returns from 1989 to 1993. Using a different time period for the regression or different return intervals (weekly or daily) for the same period can result in a different beta.
(b) Intercept of the regression = 2.09%; This is a measure of Intel's performance, when it is compared with R f (1-b). The monthly riskfree rate (since the returns used in the regression are monthly returns) between 1989 and 1993 averaged 0.4%, resulting in the following estimate for the performance -
R f (1-b) = 0.4% (1-1.39) = -0.16%
Intercept - R f (1-b) = 2.09% - (-0.16%) = 2.25%
This analysis suggests that Intel performed 2.25% better than expected, where expectations are based upon the CAPM, on a monthly basis between January 1989 and December 1993. This results in an annualized excess return of approximately 30.6%.
(c) R squared of the regression = 22.90%; This statistic suggests that 22.90% of the risk (variance) in Intel comes from market sources (interest rate risk, inflation risk ...), and tha the balance of 77.10% of the risk comes from firm-specific components. The latter should be diversifiable, and therefore unrewarded in the CAPM.

 

8. Firms which have done very well over a certain period of time will have high betas, if the betas are estimated over the same period.

( ) True

( ) False

 

Estimating CAPM Risk Parameters for General Electric

General Electric is one of the largest and most diversified industrial companies in the world, with three core areas of business - technology, which includes aircraft engines, plastics, medical systems and factory automation; services, financial, broadcasting and communications; and core manufacturing, which includes appliances, lighting, industrical and power systems. The following figure graphs monthly returns on General Electric against returns on the S&P 500 index from January 1989 to January 1994.

 


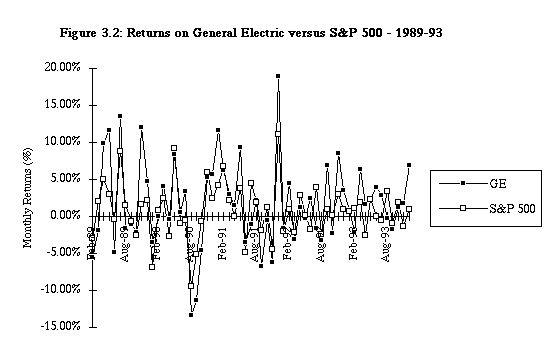
The regression statistics for GE are as follows -
(a) Slope of the regression = 1.26; This is GE's beta, based upon returns from 1989 to 1993. Using a different time period for the regression or different return intervals (weekly or daily) for the same period can result in a different beta.
(b) Intercept of the regression = 0.69%; This is a measure of GE's performance, when it is compared with R f (1-b). The monthly riskfree rate (since the returns used in the regression are monthly returns) between 1989 and 1993 averaged 0.4%, resulting in the following estimate for the performance -
R f (1-b) = 0.4% (1-1.26) = -0.10%
Intercept - R f (1-b) = 0.69% - (-0.10%) = 0.79%
This analysis suggests that GE performed 0.79% better than expected, where expectations are based upon the CAPM, on a monthly basis between January 1989 and December 1993. This results in an annualized excess return of approximately 9.90%.
(c) R squared of the regression = 60.99%; This statistic suggests that 60.99% of the risk (variance) in GE comes from market sources (interest rate risk, inflation risk ...), and tha the balance of 39.01% of the risk comes from firm-specific components.



ESTIMATION ISSUES
A. Length of Estimation Period
Most estimates of betas, including those by Value Line and Standard and Poors, use five years of data, while Bloomberg uses two years of data.
The trade-off is simple. A longer estimation period provides more data, but the firm itself might have changed in its risk characteristics over the time period.
B. Return interval.
Using daily or intra-day returns will increase the number of observations in the regression, but it opens the estimation process to a significant bias in beta estimates related to non-trading.
The betas estimated for small firms, which are more likely to suffer from non-trading, are biased downwards when daily returns are used. Using weekly or monthly returns can reduce the non-trading bias significantly .
C. Market index:
The standard practice used by most beta estimation services is to estimate the betas of a company relative to the index of the market in which its stock trades.
It may not be the best approach for an international or cross-border investor, who would be better served with a beta estimated relative to an international index.
D. Stein Estimates
Betas are often adjusted towards one to reflect estimation error and long-term trends in betas towards one.

DETERMINANTS OF BETAS
Industry Effects: The beta value for a firm depends upon the sensitivity of the demand for its products and services and of its costs to macroeconomic factors that affect the overall market. Consequently, there is a large industry effect on beta estimates. Generally speaking, the more cyclical a business, the higher the beta.

10. Consider an investment in Tiffany's, the up-upscale jewelry store. What kind of beta do you think this investment will have?

( ) Much higher than one

( ) Close to one

( ) Much lower than one



Operating Leverage Effects: Operating leverage refers to the proportion of the total costs of the firm that are fixed. Other things remaining equal, higher operating leverage results in greater earnings variability which in turn results in higher betas.

 

Measures of Operating Leverage

Fixed Costs Measure = Fixed Costs / Variable Costs

This measures the relationship between fixed and variable costs. The higher the proportion, the higher the operating leverage.

EBIT Variability Measure = % Change in EBIT / % Change in Revenues

This measures how quickly the earnings before interest and taxes changes as revenue changes. The higher this number, the greater the operating leverage.

 

11. Assume that you are comparing a European automobile manufacturing firm with a U.S. automobile firm. European firms are generally much more constrained in terms of laying off employees, if they get into financial trouble. What implications does this have for betas, if they are estimated relative to a common index?

( ) European firms will have much higher betas than U.S. firms

( ) European firms will have similar betas to U.S. firms

( ) European firms will have much lower betas than U.S. firms


Financial Leverage Effects: The beta value of a firm is a weighted average of the beta values of its debt and equity , where the weights correspond to market vales. The beta of equity alone can be written as a function of the unlevered beta and the debt-equity ratio
b L = b u (1+ ((1-t)D/E)
where
b L = Levered or Equity Beta
b u = Unlevered Beta
t = Corporate marginal tax rate
D = Market Value of Debt
E = Market Value of Equity

 

Effects of leverage on betas: Boeing Co.

In 1990, Boeing had a beta of 0.95, a debt-equity ratio of 1.71% and faced a tax rate of 34%.
Unlevered Beta = Current Beta / (1 + (1 - tax rate) (Current Debt/Equity))
= 0.95 / ( 1 + (1 - 0.34) (0.0171)) = 0.94
The levered beta at different levels of debt can then be estimated:
Levered Beta = Unlevered Beta * (1 + (1 - tax rate) (Debt/ Equity))
For instance, if Boeing were to increase its debt equity ratio to 10%, its equity beta will be
Levered Beta (@10% D/E) = 0.94 *(1+ (1 - 0.34) (0.10)) = 1.00
If the debt equity ratio were raised to 25%, the equity beta will be
Levered Beta (@25% D/E) = 0.94 *(1+ (1-0.34) (0.25)) = 1.10
D/(D+E) D/E Beta Cost of Equity
0 0 0.94 0.1417
0.1 0.1111 1.01 0.1455
0.2 0.25 1.1 0.1502
0.3 0.4286 1.21 0.1563
0.4 0.6667 1.35 0.1644
0.5 1 1.56 0.1758
0.6 1.5 1.87 0.1929
0.7 2.3333 2.39 0.2213
0.8 4 3.42 0.2782
0.9 9 6.52 0.4488


Financial And Business Risk - A Comparison
Novell RJR Nabisco
Current Beta = 1.50 Current Beta = 1.80
Debt = $0.8 million Debt = $13.927 billion
Equity = $6.4 billion Equity = $ 5.8 billion
Debt/Equity Ratio = 0 D/E Ratio = 13.93/5.8 = 2.40

Unlevered beta of Novell = 1.50 / (1+(1-0.4)(0)) = 1.50
Unlevered beta of RJR Nabsico = 1.80/(1+(1-0.4)(2.44)) = 0.74

Company Contribution from
Business Risk Financial Risk Total Risk
Novell 1.5 0 1.5
RJR Nabsico 0.74 1.06 1.8

12. Assume that you are looking at a valuation of Nabsico, and that you are also aware that Nabisco has a plan to sell of portions of its business and lower its debt. What implications, if any, does this have for the use of the beta, estimated above, in analysis?

( ) The beta comes from the regression. It should be used without any adjustments.

( ) As leverage decreases, the beta will go down. The adjusted beta should be used in the analysis.



 

BETAS BY INDUSTRY - LEVERED AND UNLEVERED

SIC Code Industry Beta D/(D+E) D/E Unlevered Beta
1 Agricultural - Crops 0.61 0.1788 0.2178 0.54
2 Agricultural Production 0.6 0.2944 0.4172 0.48
8 Forestry 0.63 0.4765 0.9102 0.41
10 Fishing, Hunting and Trappin 0.8 0.1701 0.2049 0.71
12 Coal Mining 0.93 0.3959 0.6553 0.67
13 Oil and Gas Extraction 0.66 0.247 0.3281 0.55
14 Mining of Non-metals 0.54 0.1723 0.2081 0.48
15 Building Contractors 1.14 0.3477 0.5329 0.86
16 Heavy Construction 0.74 0.2038 0.256 0.64
17 Construction- Special Trade 0.38 0.197 0.2453 0.33
20 Food and Kindred Products 0.82 0.2451 0.3246 0.69
21 Tobacco Products 1.27 0.3116 0.4527 1
22 Textile Mill Products 0.64 0.3983 0.6619 0.46
23 Apparel & Other Finished Products 0.83 0.1944 0.2414 0.73
24 Lumber & Wood Products 1.07 0.2335 0.3046 0.91
25 Furniture & Fixtures 0.93 0.2375 0.3115 0.78
26 Paper & Allied Products 0.88 0.3195 0.4696 0.68
27 Printing & Publishing 0.92 0.198 0.2468 0.8
28 Chemicals & Allied Products 1.28 0.1101 0.1238 1.19
29 Petroleum Refining 0.62 0.3395 0.5139 0.47
30 Rubber & Plastic Products 0.92 0.2533 0.3393 0.76
31 Leather & Leather Products 0.97 0.1713 0.2067 0.86
32 Stone, Clay, Glass & Concrete 0.67 0.3044 0.4376 0.53
33 Primary Metal Industries 0.96 0.3491 0.5364 0.73
34 Fabricated Metal Products 0.76 0.2413 0.3181 0.64
35 Industrial & Commercial Machinery 1.06 0.1654 0.1982 0.95
36 Electronic and Electrical Equipment 1.18 0.1225 0.1396 1.09
37 Transportation Equipment 0.9 0.3142 0.4581 0.71
38 Measuring, Analyzing & Controlling Instruments 1.13 0.1025 0.1142 1.06
39 Miscellaneous Manufacturing 0.95 0.1862 0.2288 0.84
40 Railroad Transportation 1.1 0.3777 0.607 0.81
41 Suburban Transit and Highway Transportation 1.3 0.2649 0.3604 1.07
42 Motor Freigth Transportation 0.72 0.3921 0.645 0.52
44 Water Transportation 1.07 0.4135 0.7049 0.75
45 Air Transportation 1.44 0.3731 0.5951 1.06
46 Pipelines 0.37 0.4141 0.7067 0.26
47 Transportation Services 0.85 0.2123 0.2696 0.73
48 Communications 1.13 0.256 0.344 0.94
49 Electric, Gas & Sanitary Services 0.52 0.4487 0.8138 0.35
50 Wholesale trade - Durable goods 1.01 0.2216 0.2846 0.87
51 Wholesale trade-Nondurable goods 0.98 0.2643 0.3593 0.81
52 Building materials, hardware & Garden Dealers 0.85 0.3842 0.6239 0.62
53 General Merchandise 0.95 0.374 0.5974 0.7
54 Food Stores 0.68 0.3012 0.4309 0.54
55 Auto Dealers & Gas Service Stations 1.01 0.2386 0.3133 0.85
56 Apparel & Accessory Stores 1.11 0.2222 0.2857 0.95
57 Home Furniture, Furnishings & Equip Stores 1.06 0.3365 0.5073 0.81
58 Eating & Drinking Establishments 1.06 0.2196 0.2814 0.91
59 Miscellaneous Retail 0.99 0.175 0.2122 0.88
60 Depository Institutions 1.2 0.4 0.6667 0.86
61 Non-depository Institutions 1.15 0.25 0.3333 0.96
62 Security & Commodity Brokers, Dealers .. 1.37 0.1915 0.2369 1.2
63 Insurance Carriers 0.78 0.2369 0.3104 0.66
64 Insurance Agents, Brokers & Services 0.5 0.1083 0.1215 0.47
65 Real Estate 0.5 0.2134 0.2712 0.43
67 Holding & Other Investment Services 1.03 0.1599 0.1903 0.93
70 Hotels, Rooming Houses & Lodging Places 1.22 0.3964 0.6568 0.87
72 Personal Services 1.08 0.1744 0.2112 0.96
73 Business Schools 1.36 0.0903 0.0992 1.28
75 Auto Repair, Services & parking 0.92 0.3893 0.6375 0.67
76 Miscellaneous Repair Services 1.3 0.4548 0.8343 0.87
78 Motion Pictures 0.94 0.2763 0.3817 0.76
79 Amusement & Recreation Services 1.13 0.2923 0.413 0.91
80 Health Services 1.29 0.1985 0.2476 1.13
82 Educational Services 0.67 0.1053 0.1177 0.62
83 Social Services 1.3 0.1749 0.2119 1.15
87 Engineering, Accounting, Research Services 1.28 0.1455 0.1703 1.16
89 Services not listed elsewhere 0.45 0.3419 0.5196 0.34
Average 0.93 0.2643 0.385 0.77

 

13. Assume that you have estimated the beta for Tiffany's from a regression to be 0.55. You do not believe that this is a realistic estimate. Assuming that Tiffany's debt equity ratio is 25%, can you estimate a more reasonable beta?



 

Which beta would you use in your analysis?

( ) The beta that comes from the regression.

( ) The beta estimated from above



BETAS ARE WEIGHTED AVERAGES
Case 1: Securities vs. Portfolios

Asset Market Value of holdings Weight Beta
IBM 100000 0.25 1.1
AT&T 50000 0.125 0.8
Genentech 50000 0.125 2
Real Estate 100000 0.25 0.5
Gold 100000 0.25 -0.4
PORTFOLIO 400000 1 0.65


Case 2: Effects of a takeover

14. Suppose a firm follows a policy of taking over companies in different industries with the intention of becoming a conglomerate. What will happen to its beta as it continues through this policy?

( ) The beta will go up

( ) The beta will go down

( ) The beta will converge towards one

Does it matter how the takeover is financed?


THE DISNEY/CAP CITIES MERGER

I. Before Merger
Disney: Beta = 1.15
Debt = $ 3,186 million Equity = $ 31,100 million Firm = $34,286 D/E = 0.10
ABC: Beta = 0.95
Debt = $ 615 million Equity = $ 18,500 million Firm= $ 19,115 D/E = 0.03
II. After Merger
Step 1: First calculate unlevered betas for both firms
Disney's unlevered beta = 1.15/(1+0.64*0.10) = 1.08
Cap Cities unlevered beta = 0.95/(1+0.64*0.03) = 0.93
Unlevered Beta for combined firm = 1.08 (34286/53401) + 0.93 (19115/53401)
= 1.026
[Remember to calculate the weights using the firm values of the two firms]
Step 2: Consider how the merger is financed
If Disney had used all equity to buy Cap Cities
Debt = $ 615 + $ 3,186 = $ 3,801 million
Equity = $ 18,500 + $ 31,100 = $ 49,600
D/E Ratio = 3,801/49600 = 7.66%
New Beta = 1.026 (1 + 0.64 (.0766)) = 1.08
Since Disney borrowed $ 10 billion to buy Cap Cities/ABC
Debt = $ 615 + $ 3,186 + $ 10,000 = $ 13,801 million
Equity = $ 39,600
D/E Ratio = 13,801/39600 = 34.82%
New Beta = 1.026 (1 + 0.64 (.3482)) = 1.25

FIRM BETAS VERSUS DIVISIONAL BETAS

Firm Betas as weighted averages: The beta of a firm is the weighted average of the betas of its individual projects. At a broader level of aggregation, the beta of a firm is the weighted average of the betas of its individual division.

Illustration : Decomposition of the GE Beta
General Electric is a company with several divisions, each with different risk characteristics. The following table summarizes the divisions, their market values and the divisional betas (based upon comparable firms).
The treasury bond rate is 7.5%, and the risk premium is 5.5%.

Division Market Value MV Weight Beta Cost of Equity
Financial Services $20.00 billion 0.25 0.8 0.119
Power Systems $10.00 billion 0.125 0.75 0.1163
Aircraft Engines $8.00 billion 0.1 1.25 0.1438
Industrial $10.00 billion 0.125 1.1 0.1355
Engineered Plastics $12.00 billion 0.15 1 0.13
Technical Products $8.00 billion 0.1 2 0.185
Appliances $6.00 billion 0.075 1 0.13
Broadcasting $8.00 billion 0.1 1.5 0.1575
Company $80.00 billion 1 1.13 0.1373

Note: The weighted average, from this analysis, should be equal, in theory, to the beta from the regression, but it will not because
- the firm might have changed over the five years of the regression
- there are errors in the estimates in both analyses.

 

15. If you were the chief financial officer of GE, what cost of equity would you use in capital budgeting in the different divisions?

( ) The cost of equity for GE as a company

( ) The cost of equity for each of GE's divisions

If you were the chief financial officer of GE, what cost of equity would you use in capital budgeting in the different divisions?


Estimating Betas for Non-Traded Assets

 

Using comparable firms to estimate betas

Assume that you are trying to estimate the beta for a private firm that disposes environmental and medical waste for other firms. It has a debt/equity ratio of 0.30 and a tax rate of 40%. The betas of publicly traded firms involved in environmental waste disposal are as follows (They face an average tax rate of 40%):

Firm Beta Debt/Equity
Allwaste Inc. 1.25 0.33
Browning Ferris 1.2 0.24
Chemical Waste Mgmt. 1.2 0.2
Rollins Environmental 1.35 0.02
Waste Management 1.1 0.22
Average 1.22 0.2


Unlevered Beta of environmental firms = 1.22 / (1 + (1-0.4) (0.20)) = 1.09
Beta for private firm involved in waste disposal = 1.09 (1 + (1-0.4) (0.3)) = 1.29

Divisional Beta:

The divisional betas are estimated from comparable firms.
Average Beta of the comparable firms in aircraft engines = 1.19
Average Debt/Equity Ratio of the comparable firms = 40%
Unlevered Beta of the comparable firms (based upon 36% tax rate)
= 1.19/(1+(1-0.36)(.40) = 0.947
Debt/Equity Ratio for GE Aircraft Division = 50%

Beta for GE Aircraft Division = 0.947 (1 + (1-0.36) 0.5)) = 1.25