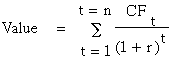
where,
n = Life of the asset
CFt = Cashflow in period t
r = Discount rate reflecting the riskiness of the estimated cashflows
* General Framework for Discounted Cash flow Valuation
* The Dividend Discount Model
- Framework
- Estimating the required rate of return
- Estimating dividends per share
- Estimating terminal price
- Present value vs. Market value
* The Free Cashflow to Equity Model
- Dividends vs. FCFE
- NCR Valuation
- Why the values are different under the two models
* Valuing a Leveraged Buyout
- What makes an LBO different?
- Approaches
- The UAL LBO
* Valuing a Restructuring
- Restructuring effects on Growth/Risk
- Valuation Consequences
DISCOUNTED CASHFLOW VALUATION
Basis for Approach
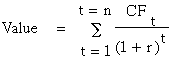
where,
n = Life of the asset
CFt = Cashflow in period t
r = Discount rate reflecting the riskiness of the estimated cashflows
Equity Valuation versus Firm Valuation
Two basic sub-approaches --
* value just the equity stake in the business
* value the entire firm, which includes, besides equity, the other claimholders
in the firm
I.Equity Valuation
The value of equity is obtained by discounting expected cashflows to
equity, i.e., the residual cashflows after meeting all expenses, tax obligations
and interest and principal payments, at the cost of equity, i.e., the rate
of return required by equity investors in the firm.
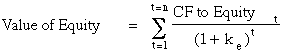
where,
CF to Equityt = Expected Cashflow to Equity in period t
ke = Cost of Equity
The dividend discount model is a specialized case of equity valuation, and
the value of a stock is the present value of expected future dividends.
II. Firm Valuation
The value of the firm is obtained by discounting expected cashflows to
the firm, i.e., the residual cashflows after meeting all operating expenses
and taxes, but prior to debt payments, at the weighted average cost of capital,
which is the cost of the different components of financing used by the firm,
weighted by their market value proportions.

where,
CF to Firmt = Expected Cashflow to Firm in period t
WACC = Weighted Average Cost of Capital
FIRST LAW OF VALUATION
Never mix and match cash flows and discount rates. The key error
to avoid is mismatching cashflows and discount rates, since discounting
cashflows to equity at the weighted average cost of capital will lead to
an upwardly biased estimate of the value of equity, while discounting cashflows
to the firm at the cost of equity will yield a downward biased estimate
of the value of the firm.
THE DIVIDEND DISCOUNT MODEL
The value of a stock in the dividend discount model is the present value
of expected dividends over time, discounted at a rate that is appropriate
for the riskiness of the expected cashflows. There are many versions of
the dividend discount model in use. We will consider only the most widely
used - the two stage dividend discount model.
Two-Stage Dividend Discount Model
The Model:
The model is based upon two stages of growth, an extraordinary growth phase
that lasts n years, and a stable growth phase that lasts forever after that:
Extraordinary growth rate: g% each year for n years ............Stable growth:
gn forever
|____________________________________________|____________________>
Value of the Stock = PV of Dividends during extraordinary phase + PV of
terminal price
![]()
where
DPSt = Expected dividends per share in year t
r = Required rate of return
Pn = Price at the end of year n
There are four basic inputs needed for the dividend discount model-
* Time Horizon for Extraordinary Growth (n): This is the period of extraordinary
growth. It will depend upon the firm being valued. The higher the current
growth rate and the more volatile the business a firm is in, the longer
the extraordinary growth period should be. As a rule of thumb,
If current growth rate is Extraordinary growth period
< 7%....... 0 years
7 - 15%... 5 years
> 15%..... 10 years
* Discount Rate (r): The cash flows that flow to equity investors should
be discounted at the cost of equity. (Remember the first principle of discounting.)
The cost of equity, in turn, will be a function of the riskiness of the
stock. If the CAPM is used,
ke = Rf + b (E(RM) - Rf)
where,
ke = Cost of Equity
Rf = Riskfree Rate
b = Beta of the stock
E(RM) - Rf = Risk Premium for
investing in risky investments
* Expected Dividends (DPSt) : The expected dividends
can be obtained by taking current dividends and applying an expected growth
to it. The better approach is to start with current earnings.
Step 1: Estimate current earnings per share
Step 2: Estimated expected growth in earnings (g) during the extraordinary
growth period.
Step 3: Estimate expected earnings per share in future periods
Step 4: Estimate dividend payout ratios for each of the future periods.
Step 5: DPSt = EPSt (1+g)t (Dividend Payoutt)
* Terminal Price (Pn): The terminal price is the expected
stock price at the end of the high growth period. It can be estimated in
one of two ways -
* Infinite Growth Model
Assumption: The growth rate after the high growth period will be
stable and remain constant forever after that. (gn
= Stable growth rate after year n)
Model: The terminal price, if the growth is stable after year n,
can be written as -
![]()
What is a stable growth rate?
As a general rule of thumb, this infinite growth rate cannot exceed the
overall growth rate for the overall economy (GNP) by more than a small amount
(2-3%). The growth rate in the overall economy can be obtained fairly simply
by adding the core long term inflation rate to the long term growth rate
in real GNP.
Estimate for the US
Upper end: Long term inflation rate (5%) + Growth rate in real
GNP (3%) =8%
Lower end: Long term inflation rate (3%) + Growth rate in real GNP (2%)
= 5%
With this estimate, the infinite growth rate cannot be greater than 10%
(8%+2%) for the upper end of the spectrum or 7% (5%+2%) for the lower end
of the spectrum.
1. You are valuing a company which is expected to have a great deal of
growth from international expansion. How would that affect your estimates
of growth during the stable growth period?
( ) I would not make any adjustment
( ) I would increase the stable growth rate substantially
( ) I would use a longer growth period and use the same stable growth rate
( ) I would not adjust the high growth period, and use a marginally higher
stable growth rate.
( ) I would use a longer growth period and a marginally higher stable growth
rate.
What is the ceiling on the expected growth?
What is a reasonable payout ratio for the terminal price calculation?
The payout ratio after the high growth period is likely to be different
from the payout ratio during the period. Intuitively, if the growth rate
is expected to decline significantly after year n. There are a couple of
ways of estimating this payout ratio -
(a) Use an average payout ratio for a stable firm (generally between 50%
and 70%)
(b) Use the fundamental growth rate formula to estimate a reasonable payout
ratio, given the stable growth rate. (See section on fundamental growth)
* Price-Earnings Ratio
Assumption: The stock will trade at the same price-earnings ratio
as the rest of the industry by the end of the high growth period.
Model:
Pn = EPSn * Average Price/Earnings
Ratio for the Industry
A Simplified Version of the Dividend Discount Model
In the case where the extraordinary growth rate (g) and payout ratio are
the same for the first n years, this formula can be simplifed as follows:
![]()
where Pn is the terminal price as defined above. This
simplifies calculations because it does not require the estimation of dividends
each year for the first n years.
More On Estimating Earnings Growth
I. Historical Growth Rates
A. Arithmetic Average versus Geometric Average
The average growth rate can be very different depending upon whether it
is an arithmetic average or a geometric average. The arithmetic average
is the mean of past growth rates, while the geometric mean takes into account
the compounding effect. The latter is clearly a much more accurate measure
of true growth in past earnings, especially when year-to-year growth has
been erratic. This can be illustrated with a simple example.
B. The Effect of Size on Growth
As firms get larger, it becomes more and more difficult to sustain high
growth rates in earnings.
II. Earnings Growth and Fundamentals
A. Earnings Growth and Return on Equity
Derivation: Define E0 to be current earnings
and _ E to be the change in earnings next year. Also define I to be the
amount invested back in the company. Then,
Earnings Growth rate = _ E / E0
= (I/ E0) * (_ E / I)
= (1 - payout ratio) * (ROE)
= b* ROE
Implications: The earnings growth rate of a company is an increasing
function of
- the amount reinvested back in the company, i.e. retention ratio 'b'
- the quality of investments in which the money is reinvested, i.e. ROE.
2. You attempting to estimate expected growth for The Gap and J.P. Morgan.
The Gap has a return on equity of 25% and pays out 30% of its earnings as
dividends. J.P. Morgan has a return on equity of 15% and pays out 50% of
its earnings as dividends. Estimate the expected growth rate for each of
these companies ñ
( ) The Gap's expected growth =
( ) J.P. Morgan's expected growth =
What is the ceiling on the expected growth?
B. Return on Equity and Leverage
The return on equity, and by implication, the growth rate, are affected
by the leverage decisions of the firm. In the broadest terms, increasing
leverage will lead to a higher return on equity if the pre-interest, after-tax
return on projects (assets) exceeds the after-tax interest rate paid on
debt. This is captured in the following formulation of return on equity:
ROE = ROA + D/E (ROA - i (1-t))
where,
ROA = (Net Income + Interest (1 - tax rate)) / (BV of Debt+BV of Equity)
= EBIT (1- t) / BV of Debt and Equity
D/E = Debt/ Equity (Market Value if available)
i = Interest Expense on Debt / BV of Debt
t = Tax rate on ordinary income
The derivation is simple and is provided in a footnote. Using this expanded
version of ROE, the growth rate can be written as:
g = b (ROA + D/E (ROA - i (1-t))
The advantage of this formulation is that is allows explicitly for changes
in leverage and the consequent effects on growth. It is a useful way of
analyzing the effects of restructuring on growth and value.
3. Assume that you estimating the effect of a recent restructuring at
Rubbermaid on expected growth. Rubbermaid has a return on assets of 18%,
has no leverage and pays out 20% of its earnings as dividends. It is planning
to sell of low-return assets and increase its return on assets to 20%, increase
its debt equity ratio to 25% and pay 30% of its earnings as dividends. The
tax rate is 40%, and the pre-tax borrowing rate is 10%. Estimate the expected
growth before and after the restructuring.
( ) E(growth) before restructuring =
( ) E(growth) after restructuring =
Does the higher growth automatically mean that the value of the stock will
increase?
( ) Yes
( ) No
Estimating Payout Ratio for Stable Growth Period
The payout ratio after the high growth period can be estimated, based upon
the stable growth rate and the fundamentals of the firm.
Payout Ratio during Stable Phase = 1 - (gn/ (ROA + D/E (ROA-i(1-t)))
where,
gn = Stable Growth Rate
ROA = Return on Assets during stable growth period
D/E = Debt / Equity Ratio
i = Interest rate on debt
4. Consider the example of Rubbermaid described above. Given the ROA of
20%, the debt equity ratio of 25% and the pre-tax cost of debt of 10%, estimate
the payout ratio that Rubbermaid can afford to have, given the expected
growth rate of 6%.
r Payout Ratio in Stable Phase =
Why is the payout ratio so high?
III. Analyst Forecasts of Growth
How good are analysts at forecasting earnings?
Box- Jenkins: is a simple time series model for forecasting earnings
per share using past EPS.
Studies seem indicate that analysts are better at forecasting earnings than
simple time series models.
The Accuracy of Short Term Forecasts
The general consensus from studies that have looked at short-term forecasts
(one quarter ahead to four quarters ahead) of earnings is that analysts
provide better forecasts of earnings than models that depend purely upon
historical data. The following table summarizes the results from three studies
of analysts forecasts.
Mean Relative Absolute Error
Study Analyst Group Analyst Mechanical
Forecasts Models
Collins & Hopwood Value Line Forecasts 31.7% 34.1%
1970-74
Brown & Rozeff Value Line Forecasts 28.4% 32.2%
1972-75
Fried & Givoly Earnings Forecaster 16.4% 19.8%
1969-79
The mean relative absolute error measures the absolute difference between
the actual earnings and the forecast for the next quarter, in percentage
terms. The mechanical models are all based upon historical data.
* Does The Dividend Discount Model Work?
Study inputs:
Current EPS = Average of last five years of earnings
Discount rate = CAPM adjusted return
Intermediate growth rate = IBES Analysts forecasts of earnings growth
Terminal growth rate = 8 % for all stocks
Payout ratio = Set equal to 45 % even for companies that do not pay dividends
Results:

THE FREE CASHFLOW TO EQUITY MODEL
A. FCFE vs Dividends
FCFE is what the company has available to pay out as dividends. The free
cashlfow to equity is the cashflow left over after working capital and capital
investment needs:
Item Assumptions
Net Income : Net profit after taxes
- (Cap Ex - Deprec'n) * (1 - DR) : Capital investment needs * (1 - Debt
Ratio)
- Chg in Working Capital * (1 - DR) : D Working
Capital * (1 - Debt Ratio)
= Free Cashflows to Equity : Cashflows available to equity investors
B. The Two-stage Model
The value of any stock is the present value of the FCFE per year for the
extraordinary growth period plus the present value of the terminal price
at the end of the period.
Value = PV of FCFE + PV of terminal price
= Sum of FCFEt / (1+r)t + Pn / (1+r)n
where,
FCFEt = Free Cashflow to Equity in year t
Pn = Price at the end of the extraordinary growth period
r = Required rate of return to equity investors in the firm
The terminal price is generally calculated using the infinite growth rate
model,
Pn = FCFEn+1 / (r - gn)
where,
gn = Growth rate after the terminal year forever.
C. Calculating the terminal price
If infinite growth rate model used:The same caveats that apply to
the growth rate for the Gordon Growth Rate model (within 2% of growth rate
in nominal GNP) apply here as well. In addition, the free cashflow to equity
after the terminal year has to be consistent with this assumption of stable
growth rate. A strong implication of this is that capital spending and depreciation
have to be in rough parity. (Some even suggest that they should offset each
other) A stable firm cannot be spending twice as much on equipment each
year as it is getting back from depreciation.
5. Many analysts assume that capital expenditures offset depreciation,
when doing valuation. Is it an appropriate assumption to make for a high
growth firm?
( ) Yes
( ) No
What about a stable growth firm?
( ) Yes
( ) No
VALUING NCR USING DIVIDEND DISCOUNT MODEL AND THE FCFE MODEL
Step 1: Estimate the required rate of return for stockholders
| Beta= | 1.15 | T.Bond Rate = | 9.00% | |
| Exp. Return = | 15.33% | Market risk premium = | 5.50% |
Current Earnings per Share = $5.43
Dividend Payout Ratio = 26.00% Retention Ratio = 74%
Return on Assets
= (Net Income + Interest Expenses (1-tax rate) / (BV: Debt + BV: Equity)
= ( $369 + $40 (1-0.34))/(537+1850) = 16.56%
Debt Equity Ratio = Debt/Market Value of Equity = 537/(88*67.96)
= 8.98%
Interest Rate on Debt = 7.45%
Expected Growth Rate in Earnings
= Retention Ratio ( ROA + D/E (ROA - i (1-t))
= 0.74 (16.56% + .0898 (16.56% - 7.45% (1-0.34))
= 13.03%
[In comparison, the historical growth rate was 11.51% and the analyst projection
was 9.50%]
Year |
EPS |
DPS |
1 |
$6.14 |
$1.60 |
2 |
$6.94 |
$1.80 |
3 |
$7.84 |
$2.04 |
4 |
$8.86 |
$2.30 |
5 |
$10.02 |
$2.60 |
Current Revenues per share = $92.60
Current Capital Expenditures = $6.20 Current Depreciation = $4.41
Working Capital as a percent of revenues = 15% (Averaging 1990-92 numbers)
Debt Financing used to finance investment needs = 537/(537 + 88*67.96)
= 8.24%
Capital expenditures, depreciaton and revenues are expected to grow at the
same rate as earnings (13.03%).
Year |
Depreciation |
Capital Expenditures |
(Cex-Depr)(1-_) |
D WC (1-_) |
1 |
$4.99 |
$7.01 |
$1.85 |
$1.66 |
2 |
$5.64 |
$7.92 |
$2.09 |
$1.88 |
3 |
$6.38 |
$8.95 |
$2.37 |
$2.12 |
4 |
$7.21 |
$10.12 |
$2.67 |
$2.40 |
5 |
$8.15 |
$11.44 |
$3.02 |
$2.71 |
Year |
EPS |
(Cex-Depr)(1-_) |
D WC (1-_) |
FCFE/sh |
1 |
$6.14 |
$1.85 |
$1.66 |
$2.63 |
2 |
$6.94 |
$2.09 |
$1.88 |
$2.97 |
3 |
$7.84 |
$2.37 |
$2.12 |
$3.36 |
4 |
$8.86 |
$2.67 |
$2.40 |
$3.79 |
5 |
$10.02 |
$3.02 |
$2.71 |
$4.29 |
Growth rate after year 5 = 6%
Beta after year 5 = 1.00
ROA after year 5 = 15.00%
D/E ratio and interest rate are expected to remain unchanged.
Expected Payout Ratio after year 5
= 1 - Expected Growth Rate/ ( ROA + D/E (ROA - i (1-t))
= 1 - 6% / (.15 + 0.0898 (.15 - .0745 (1-.34)) = 62.28%
Terminal Price from the Dividend Discount Model
= EPS5 * (1+gn) * Stable Payout
Ratio / (r - gn)
= $10.02(1.06)(.6228)/(.145-.06) = $ 77.81
Capital Expenditures are expected to offset depreciation after year 5
Working Capital will continue to remain at 15% of Revenues
FCFE in year 6 = EPS6 - (Capital Expenditures6 - Depreciation6)(1-_) - D
WC(1-_)
= $10.02(1.06) - $0 - $1.54(1-.0824) = $9.21
D WC =[ (Revenues6 - Revenues5)*WC as % of Revenues]/Number of Shares = $1.54
Terminal Price = $9.21/(.145-.06) = $ 108.36
Step 5 : Calculate the present value
Year |
DPS |
TERM. PR. |
FCFE/sh |
Term. Val. |
1 |
$1.60 |
$2.63 |
||
2 |
$1.80 |
$2.97 |
||
3 |
$2.04 |
$3.36 |
||
4 |
$2.30 |
$3.79 |
||
5 |
$2.60 |
$77.81 |
$4.29 |
$108.36 |

FCFE Valuation versus Dividend Discount Model Valuation
a. When they are similar
* Where the dividends are equal to the FCFE
* Where the FCFE is greater than dividends, but the excess cash (FCFE -
Dividends) is invested in projects with net present value of zero.
b. When they are different
When dividends are less than FCFE
* When the FCFE is greater than the dividend and the excess cash either
earns below-market interest rates or is invested in negative net present
value projects, the value from the FCFE model will be greater than the value
from the dividend discount model.
* The payment of smaller dividends than can be afforded to be paid out lowers
debt-equity ratios and may lead the firm to become underleveraged, causing
a loss in value.
When dividends are greater than FCFE
* Flotation cost on new equity issues creates an expense which decreases
value.
* If the firm borrows the money to pay the dividends, the firm may become
overleveraged (relative to the optimal) leading to a loss in value.
* Paying too much in dividends can lead to capital rationing constraints
where good projects are rejected, resulting in a loss of wealth.
c. What does it mean when they are different?
* Difference between the value from the FCFE model and the value using the
dividend discount model can be considered one component of the value of
controlling a firm - it measures the value of controlling dividend policy.
VIII & IX. TWO AND THREE STAGE VERSIONS OF THE FCFF MODEL
The Model
The value of the firm, in the most general case, can be written as the present
value of expected free cashflows to the firm:
Value of Firm = ![]()
where,
FCFFt = Free Cashflow to firm in year t
WACC = Weighted average cost of capital
If the firm reaches steady state after n years, and starts growing at a
stable growth rate gn after that, the value of the
firm can be written as:
Value of Firm = ![]()
Firm Valuation versus Equity Valuation
(a) Consistent assumptions are made about growth in the two approaches
(b) Bonds are correctly priced
Best suited for:
Illustration: Federated Department Stores: Valuing an over-leveraged
firm using the FCFF approach
A Rationale for using the Two-Stage FCFF Model
Background Information
Valuation
The forecasted free cashflows to the firm over the next five years are provided
below:
1 |
2 |
3 |
4 |
5 |
Terminal year | |
| EBIT | $574.45 |
$620.41 |
$670.04 |
$723.64 |
$781.54 |
$820.61 |
| - t (EBIT) | $ 206.80 |
$223.35 |
$241.21 |
$260.51 |
$281.35 |
$295.42 |
| - (Cap Ex - Depreciation) | $111.24 |
$120.14 |
$129.75 |
$140.13 |
$151.34 |
$0.00 |
| - Ch Working Capital | $144.58 |
$156.15 |
$168.64 |
$182.13 |
$196.70 |
$132.77 |
| = FCFF | $101.83 |
$120.77 |
$130.44 |
$140.87 |
$152.15 |
$392.42 |
| PV of FCFF | $487.17 |
| PV of Terminal Value = | $3,946.93 |
| Value of Firm = | $4,434.11 |
| Value of Debt = | $2,740.58 |
| Value of Equity = | $1,693.52 |
| Value Per Share = | $13.38 |
SPECIAL CASES IN VALUATION
* Cyclical or Troubled Firms: There are two general problems in
valuing these firms-
- Current earnings are generally depressed and in many cases negative. When
earnings are depressed, using them in valuation will result in very low
values. When they are negative, it becomes even more difficult.
- Historical growth rates are negative and often meaningless.
In these cases, earnings have to be normalized. There are a number of different
ways of doing this -
(a) If earnings are depressed purely because of the economic cycle, and
are expected to rebound once the economy recovers:
* The standard approach is to average income over a period long enough to
include an economic recovery and a recession.
* A variant on this approach that allows for scaling to size is to calculate
the average return on equity or return on assets over the period. This return
on equity is applied to the current book value of equity to arrive at a
standardized net income. Alternatively, the return on assets is applied
to the current book value of assets to arrive at a standardized after tax
operating income.
Example: Ford Motor Company reported earnings per share of -$0.73
in 1992, in the midst of the recession. The following are estimated normalized
earnings per share using both the average income and average r