The Adjusted Present Value Approach
In
the adjusted present value (APV) approach, we begin with the value of the firm
without debt. As we add debt to the firm, we consider the net effect on value
by considering both the benefits and the costs of borrowing. To do this, we
assume that the primary benefit of borrowing is a tax benefit and that the most
significant cost of borrowing is the added risk of bankruptcy.
The
Mechanics of APV Valuation
We
estimate the value of the firm in three steps. We begin by estimating the value
of the firm with no leverage. We then consider the present value of the
interest tax savings generated by borrowing a given amount of money. Finally,
we evaluate the effect of borrowing the amount on the probability that the firm
will go bankrupt, and the expected cost of bankruptcy.
Value
of Unlevered Firm
The
first step in this approach is the estimation of the value of the unlevered
firm. This can be accomplished by valuing the firm as if it had no debt, i.e.,
by discounting the expected free cash flow to the firm at the unlevered cost of
equity. In the special case where cash flows grow at a constant rate in
perpetuity, the value of the firm is easily computed.
Value of Unlevered Firm = ![]()
where
FCFF0 is the current after-tax operating cash flow to the firm, ru
is the unlevered cost of equity and g is the expected growth rate. In the more
general case, you can value the firm using any set of growth assumptions you
believe are reasonable for the firm.
The
inputs needed for this valuation are the expected cashflows, growth rates and
the unlevered cost of equity. To estimate the latter, we can draw on our
earlier analysis and compute the unlevered beta of the firm.
![]()
where
bunlevered
= Unlevered beta of the firm
bcurrent
= Current equity beta of the firm
t = Tax rate for the firm
D/E = Current debt/equity ratio
This
unlevered beta can then be used to arrive at the unlevered cost of equity.
Expected
Tax Benefit from Borrowing
The
second step in this approach is the calculation of the expected tax benefit
from a given level of debt. This tax benefit is a function of the tax rate of
the firm and is discounted at the cost of debt to reflect the riskiness of this
cash flow. If the tax savings are viewed as a perpetuity,
Value
of Tax Benefits 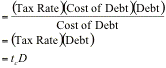
The
tax rate used here is the firmÕs marginal tax rate and it is assumed to stay
constant over time. If we anticipate the tax rate changing over time, we can
still compute the present value of tax benefits over time, but we cannot use the
perpetual growth equation cited above.
Estimating
Expected Bankruptcy Costs and Net Effect
The
third step is to evaluate the effect of the given level of debt on the default
risk of the firm and on expected bankruptcy costs. In theory, at least, this requires
the estimation of the probability of default with the additional debt and the
direct and indirect cost of bankruptcy. If pa is the
probability of default after the additional debt and BC is the present value of
the bankruptcy cost, the present value of expected bankruptcy cost can be
estimated.
PV
of Expected Bankruptcy cost ![]()
This
step of the adjusted present value approach poses the most significant
estimation problem, since neither the probability of bankruptcy nor the bankruptcy
cost can be estimated directly.
There
are two basic ways in which the probability of bankruptcy can be estimated
indirectly. One is to estimate a bond rating, as we did in the cost of capital
approach, at each level of debt and use the empirical estimates of default
probabilities for each rating. For instance, Table 15.8, extracted from a study
by Altman and Kishore, summarizes the probability of default over ten years by
bond rating class in 1998.[1]
Table
15.8: Default Rates by Bond Rating Classes
|
Bond Rating |
Default Rate |
|
D |
100.00% |
|
C |
80.00% |
|
CC |
65.00% |
|
CCC |
46.61% |
|
B- |
32.50% |
|
B |
26.36% |
|
B+ |
19.28% |
|
BB |
12.20% |
|
BBB |
2.30% |
|
A- |
1.41% |
|
A |
0.53% |
|
A+ |
0.40% |
|
AA |
0.28% |
|
AAA |
0.01% |
Source: Altman and Kishore (1998)
The
other is to use a statistical approach, such as a probit to estimate the probability of default,
based upon the firmÕs observable characteristics, at each level of debt.
The
bankruptcy cost can be estimated, albeit with considerable error, from studies
that have looked at the magnitude of this cost in actual bankruptcies. Research
that has looked at the direct cost of bankruptcy concludes that they are small[2], relative to firm value. The indirect
costs of bankruptcy can be substantial, but the costs vary widely across firms.
Shapiro and Titman speculate that the indirect costs could be as large as 25%
to 30% of firm value but provide no direct evidence of the costs.
Illustration
15.5: Valuing a firm with the APV approach: Tube Investments
In
Illustration 15.1, we valued Tube Investments, using a cost of capital
approach. Here, we re-estimate the value of the firm using an adjusted present
value approach in three steps.
Step
1: Unlevered firm value
To
estimate the unlevered firm value, we first compute the unlevered beta. Tube
InvestmentÕs beta is 1.17, its current market debt to equity ratio is 79% and
the firmÕs tax rate is 30%.
Unlevered
beta = ![]()
Using
the rupee riskfree rate of 10.5% and the risk premium of 9.23% for India, we
estimate an unlevered cost of equity.
Unlevered
cost of equity = 10.5% + 0.75(9.23%) = 17.45%
Using
the free cash flow to the firm that we estimated in Illustration 15.1 of Rs
212.2 million and the stable growth rate of 5%, we estimate the unlevered firm
value:
Unlevered
firm value= ![]()
Step
2: Tax benefits from debt
The
tax benefits from debt are computed based upon Tube InvestmentÕs existing
dollar debt of Rs. 1807.3 million and the tax rate of 30%:
Expected
tax benefits in perpetuity = Tax rate (Debt) = 0.30 (1807.3) = Rs 542.2 million
Step
3: Expected bankruptcy costs
To
estimate this, we made two assumptions. First, based upon its existing rating,
the probability of default at the existing debt level is 10%. Second,the cost
of bankruptcy is 40% of unlevered firm value.
Expected
bankruptcy cost =Probability of bankruptcy * Cost of bankruptcy * Unlevered
firm value = 0.10*0.40*1704.6 = Rs 68.2 million
The
value of the operating assets of the firm can now be estimated.
Value
of the operating assets
=
Unlevered firm value + PV of tax benefits Š Expected Bankruptcy Costs
=
1704.6 + 542.2 Š 68.2 = Rs 2178.6 million
Adding
to this the value of cash and marketable securities of Rs. 1365.3 million, we
obtain a value for the firm of Rs 3543.9 million. In contrast, we valued the
firm at Rs. 3367.3 million with the cost of capital approach.
Cost
of Capital versus APV Valuation
In an APV valuation, the value of a
levered firm is obtained by adding the net effect of debt to the unlevered firm
value.
Value of Levered Firm = ![]()